ベジェ曲線は、ベクタ形式の画像で曲線を表現するのに使われています。フォントのアウトラインもベジェ曲線の集まりです。ベジェ曲線で表現されるのは一つの曲線の区間だけです。大抵は複数のベジェ曲線が集まって一つの図形を表現します。
ベジェ曲線には制御点の個数によって2次ベジェ、3次ベジェなどが存在します。グラフィックソフトで使われるのは2次, 3次がほとんどです。
ドローソフト等を扱っていると慣れ親しむことになるベジェ曲線ですが、その線がどのように計算されるかについては感覚的にしかとらえられていない場合がほとんどなのではないでしょうか。ここでは、2次、3次のベジェ曲線を手で描いてみようと思います。自分で描いてみることで、その動作に理解を深めることができるかもしれません。ベジェ曲線上の点を求める方法は、ド・カステリョ(De Casteljau)のアルゴリズムを元にしています。
2次ベジェ

まずは2次のベジェ曲線を考えます。2次のベジェ曲線には3つの制御点が存在します。
曲線の両端の制御点から、真ん中の制御点に近づくような曲線になります。
2次ベジェ曲線は TrueType フォントのアウトラインに使われています*1。
描き方
まず、適当に制御点3点を決めてプロットします。
3つの点を順に とします。
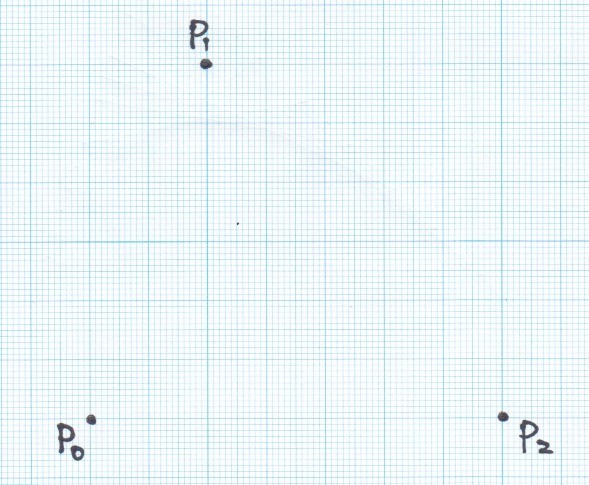
間をそれぞれ結びます。

4等分
次に、線分 をそれぞれ4等分します。

線分 をそれぞれ 1:3 に内分する点を結びます。

結んだ線分を 1:3 に内分する点を求めます。この点が求めるベジェ曲線上の点になります。

補助線を消すと

同様に線分 をそれぞれ 3:1 に内分する点を結び、結んだ線分をさらに 3:1 で内分した点を求めます。

補助線を消すと

8等分
次に、同様に線分 をそれぞれ8等分した点を追加します。

線分 をそれぞれ 1:7 に内分する点を結び、結んだ線分をさらに 1:7 で内分した点を求めます。

以下同様に 3:5 で内分する場合

5:3 の場合

7:1 の場合

補助線を消すと
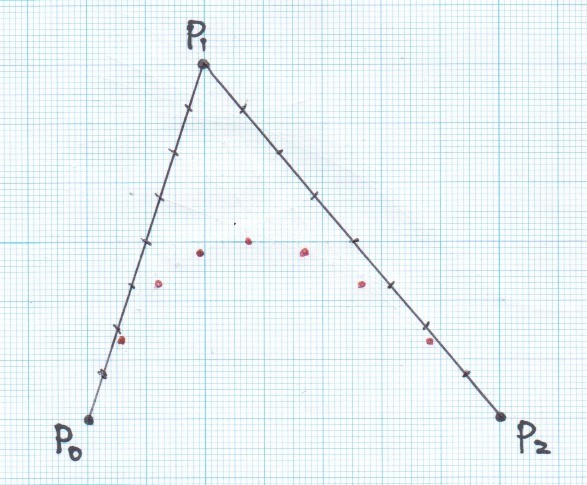
だんだん形が見えてきました。
16等分
次に、同様に線分 をそれぞれ16等分する点を追加します。

同様にベジェ曲線上の点を求めていきます。
1:15 の場合

3:13 の場合

5:11 の場合

7:9 の場合

9:7 の場合

11:5 の場合

13:3 の場合

15:1 の場合
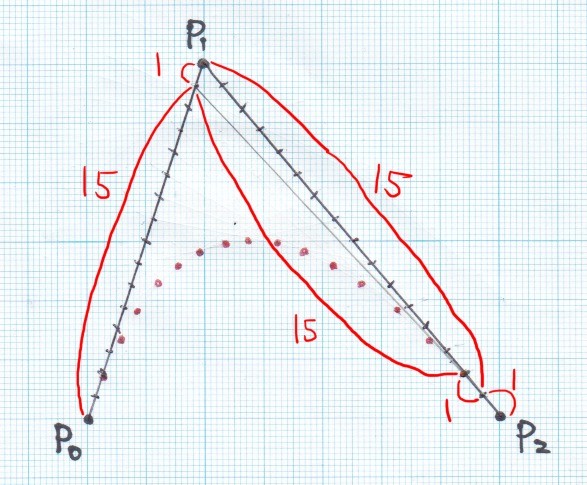
補助線を消すと

求めた点を滑らかに結ぶと、だいたい求めるベジェ曲線になります。

また、ここではベジェ曲線上の点を求める際に引いた補助線を毎回消していましたが、補助線をすべて残したままにすると次のようになります。
2次ベジェ曲線は、引いた全ての補助線の内側に接するような曲線になります。
8等分

16等分

一般化: パラメータ t
さて、一般化します。
ある実数 について、線分
をそれぞれ
に内分する点を
とします。
次に、線分 を結びます。線分
を
に内分する点
が求めるベジェ曲線上の点になります。
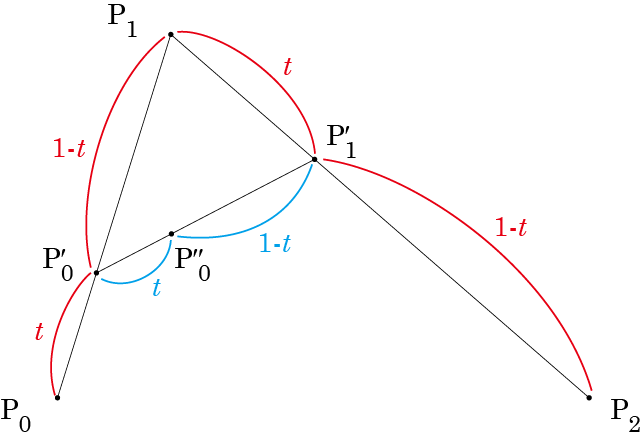
制御点列 で規定される2次ベジェ曲線は、2組の制御点列
で規定される2つの2次ベジェ曲線に分割することができます。この分割手法をド・カステリョ(De Casteljau)のアルゴリズムといいます。
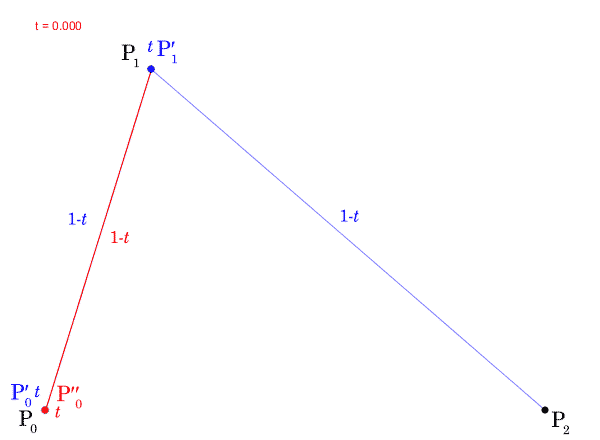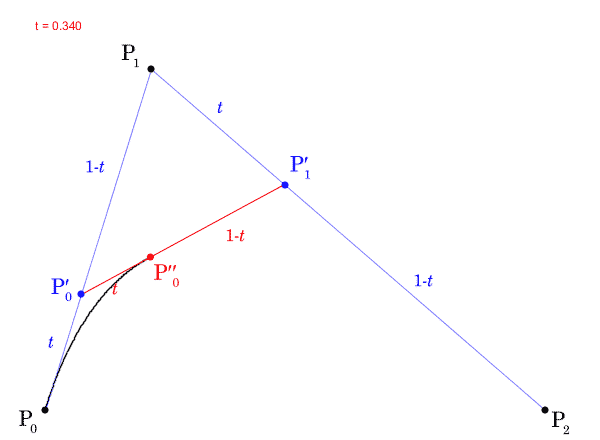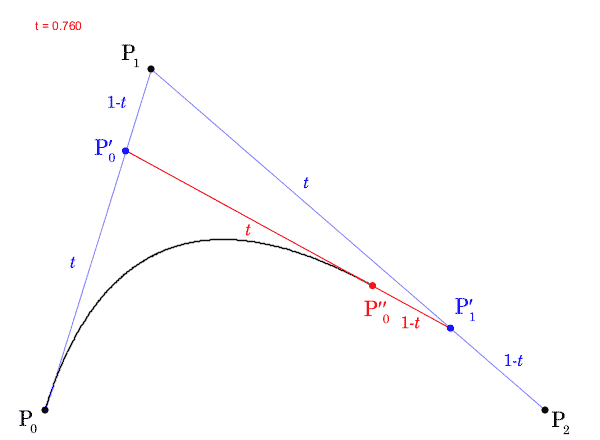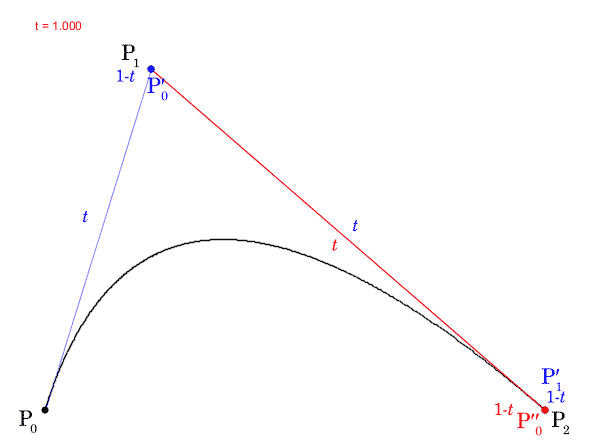
ここで、 の値を
から
まで動かすと、点
の軌跡はベジェ曲線になります。実際に
の値を
から
まで動かした時の点
の軌跡を描いたGIF動画を次に示します。
は曲線上の点の位置を指定し、パラメータと呼ばれます。
また、この の座標
は、次の式によって与えられます。ただし
は制御点の座標を示すベクタです。
3次ベジェ
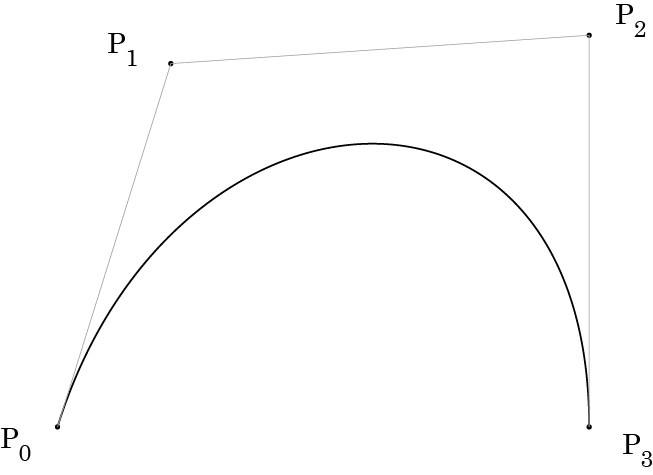
3次ベジェは4つの制御点からなります。両端の点の間に2つの制御点がはさまる感じです。
Illustratorや、PostScriptフォントのアウトライン表現で使われています。
次の4つの制御点で定められるベジェを描いてみようと思います。

これは、実際にイラストレータで制御点をこの位置に指定すると次のような曲線になります。

では、次から実際に描いてみましょう。次からベジェ曲線上の点を求めていきますが、ある程度の個数求まったらなめらかな線で結ぶと概形が得られます。
半分
まず、制御点 を結びます。

線分 をそれぞれ二等分します。
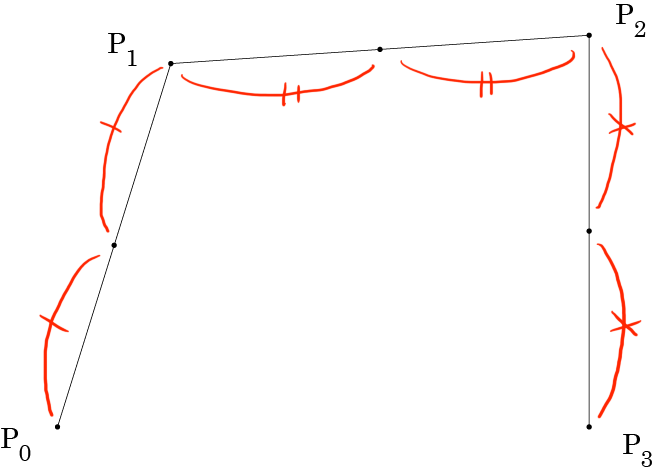
二等分した点を次図のように結びます。
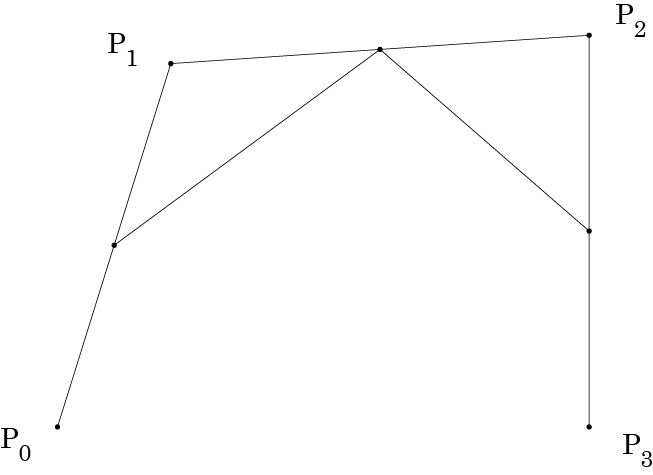
2等分した点を結んだ線分2つについて、その2等分点同士を結びます。
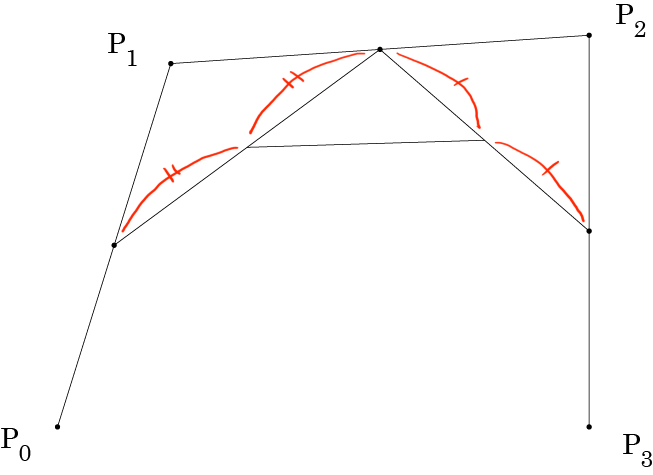
結んだ線分を2等分する点が、求める3次ベジェ曲線上の点になります。

引いた補助線を消すと

これで一点を求めることができました。
4等分
次にすすみます。
線分 をそれぞれ4等分する点を追加します。
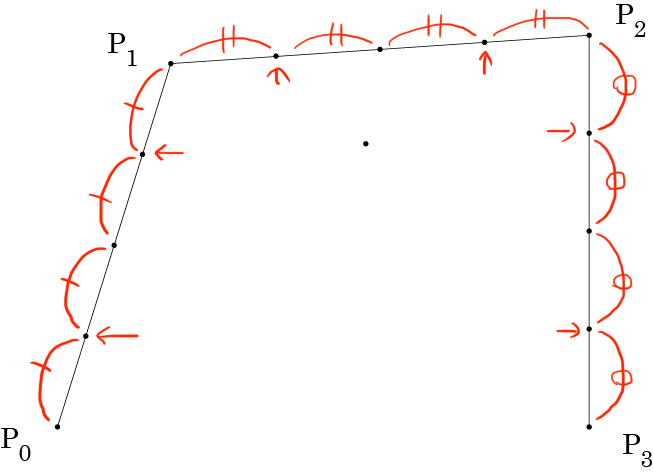
それらの線分を1:3に内分する点を次のように結びます。
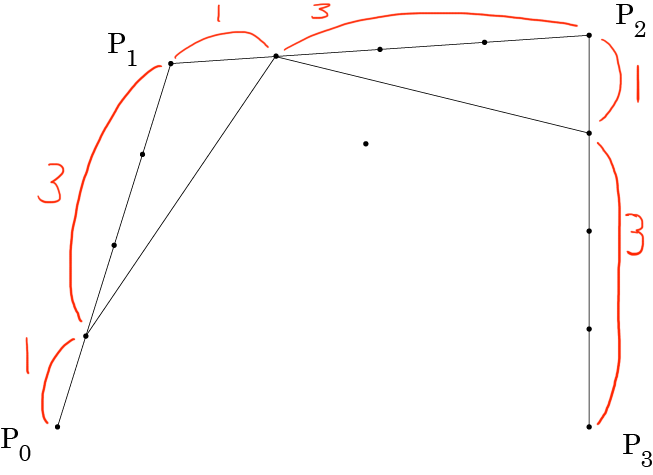
さらに、先の図で結んだ線分2つについて、それぞれを 1:3 で内分する点を結びます。
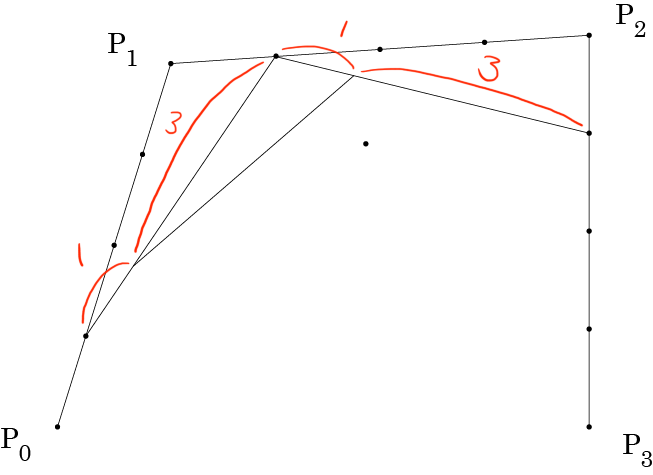
結んだ線分を 1:3 に内分する点が求めるベジェ曲線上の点になります。
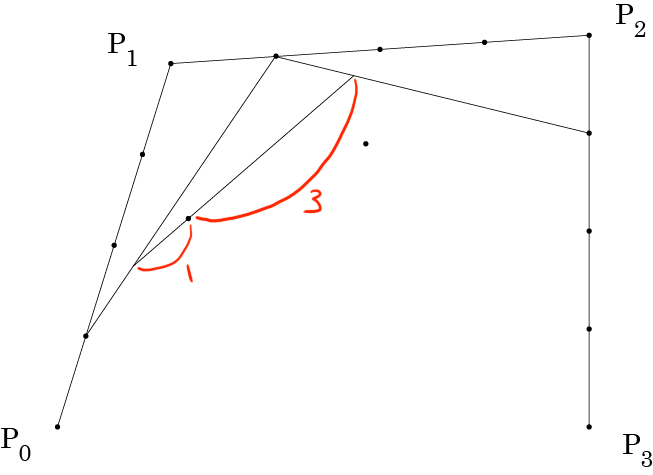
補助線を消すと

次の点も同様に描きます。ただし今度は線分を 3:1 で内分することになります。

補助線を消すと

8等分
次も同様です。
線分 をそれぞれ8等分する点を追加します。

順にベジェ曲線上の点を求めていきます。
1:7で内分するとき

3:5のとき

5:3のとき

7:1のとき

だんだんと曲線の形が見えてきました。

16等分
次も同様に線分 をそれぞれ16等分する点を追加します。
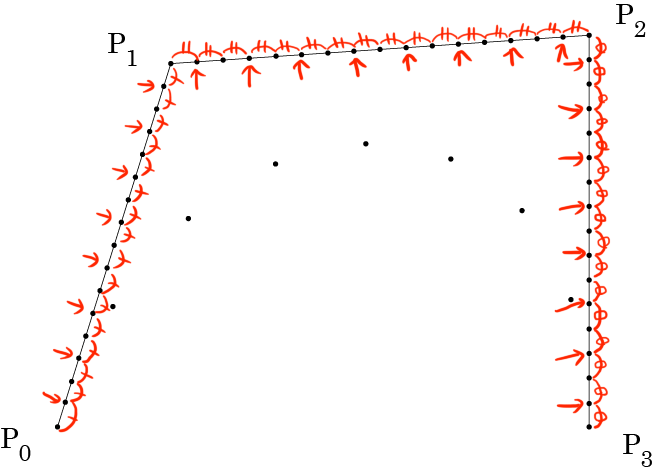
また同様にベジェ曲線上の点を求めていきます。
1:15
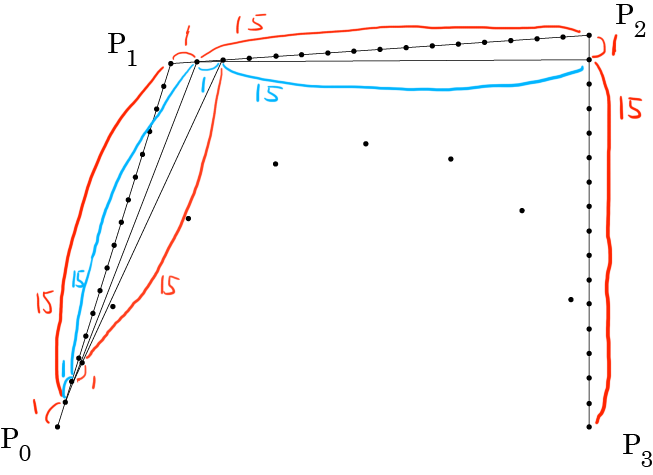
3:13

5:11
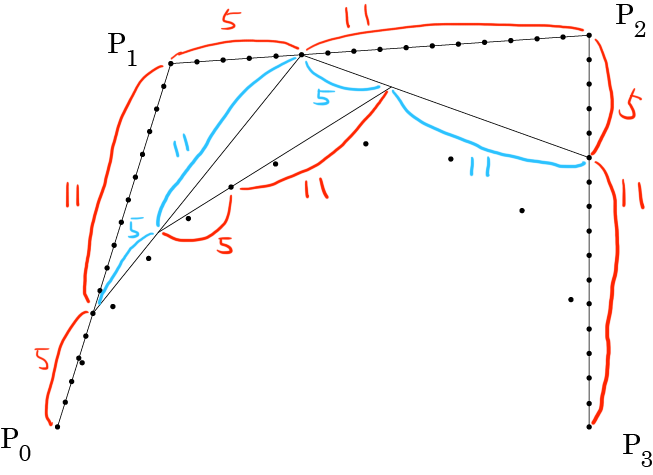
7:9
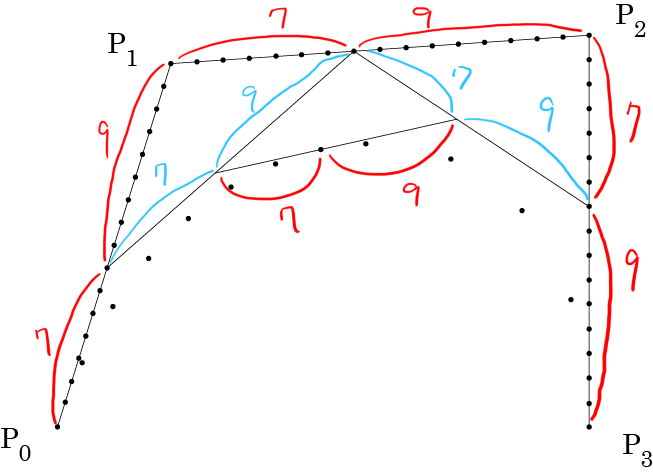
9:7
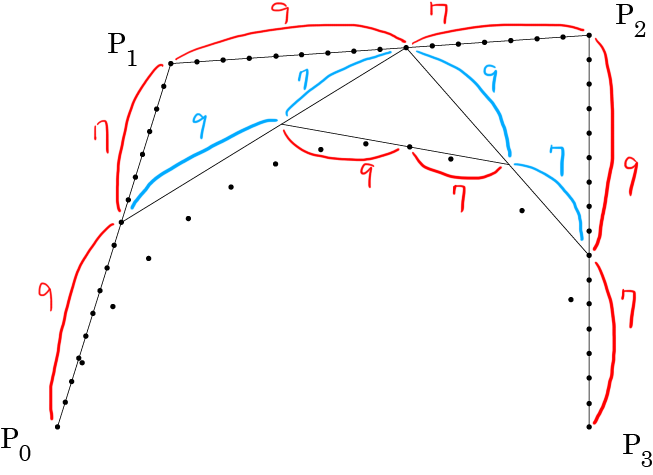
11:5
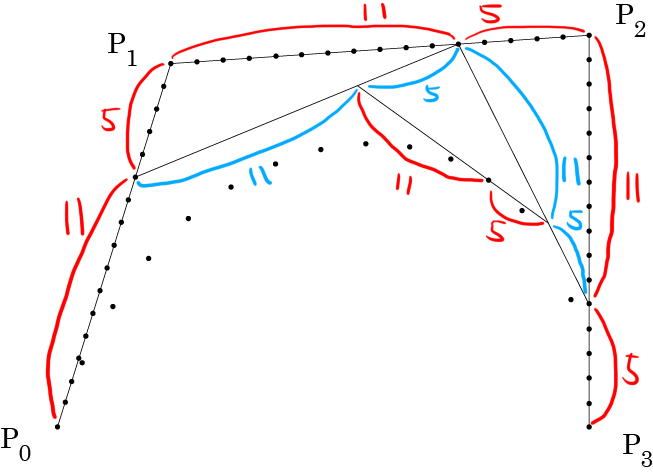
13:3
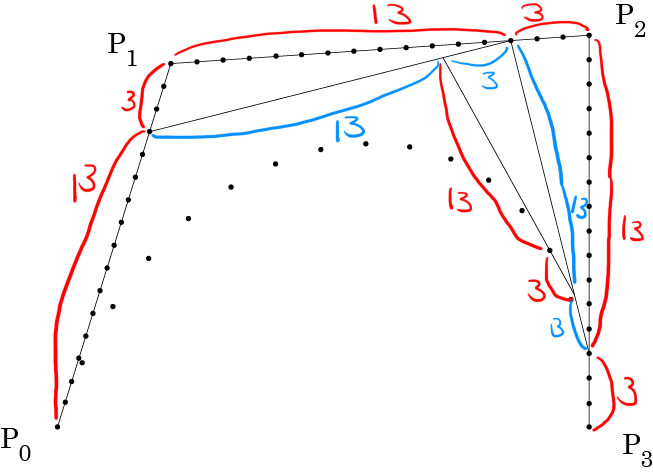
15:1
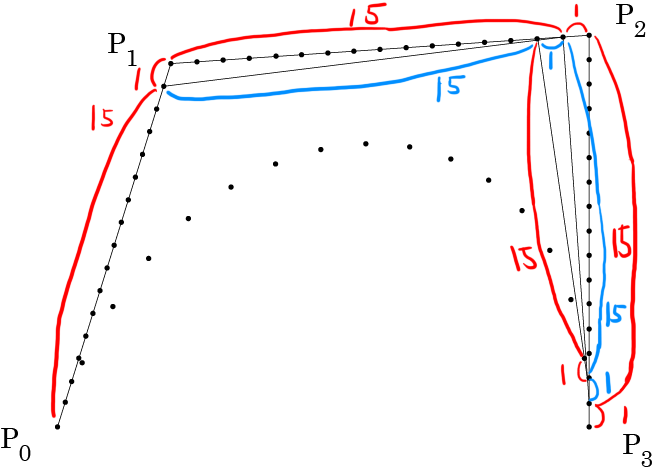
結果、この様になります。

32等分
32等分点についても対応する点を求めると次のようになります。

求めた点をイラストレーターによるベジェ曲線と重ねてみると、これらの点がベジェ曲線上にあることがわかります。

また、点を求めるのに使用した全ての補助線を表示させると次のようになります。

これをみると、求める3次ベジェ曲線のおおよその形が見えます。それに加え、 および
によって定義される2次ベジェ曲線の形が見えます。これは、
の内分点同士を結んだ線を内分した点を求めることが、2次ベジェ上の点を求める方法と同一だからです。
一般化: パラメータ t
さて、一般化します。
パラメータとなる実数 を考えます。
ある について、線分
をそれぞれ
に内分する点を
とします。
次に、線分 を結びます。線分
をそれぞれ
に内分する点を
とします。
線分 を結びます。線分
を
に内分する点
が求めるベジェ曲線上の点になります。

ここで、 の値を
から
まで動かし、点
の軌跡を描いたGIF動画を次に示します。
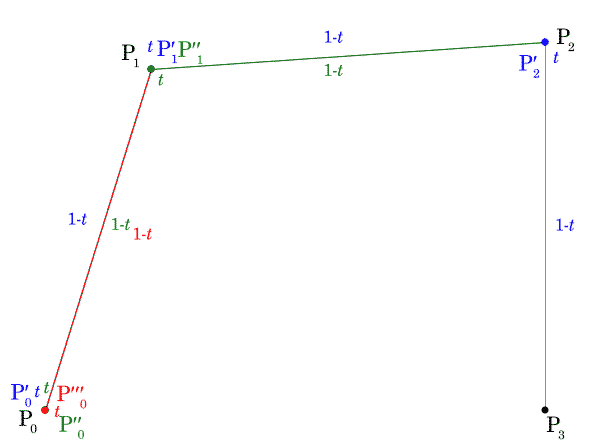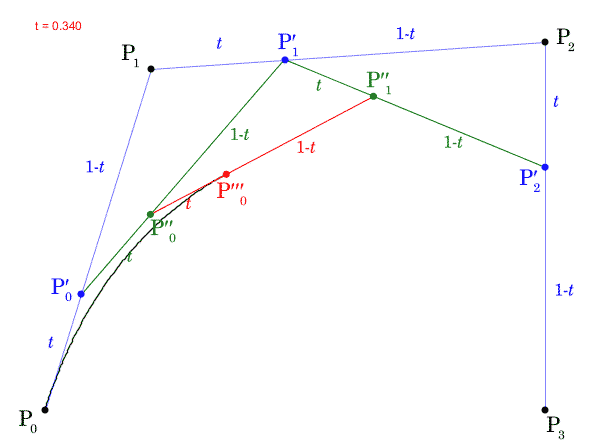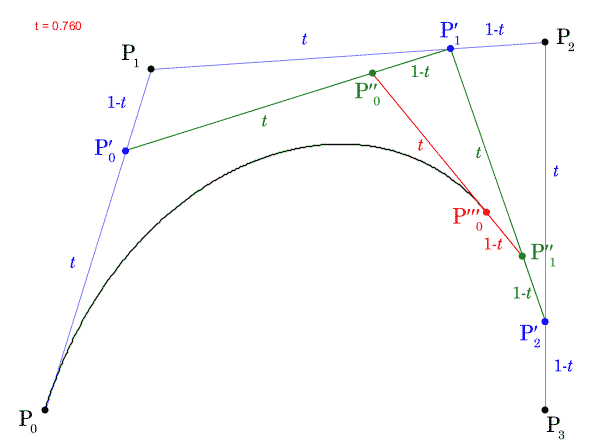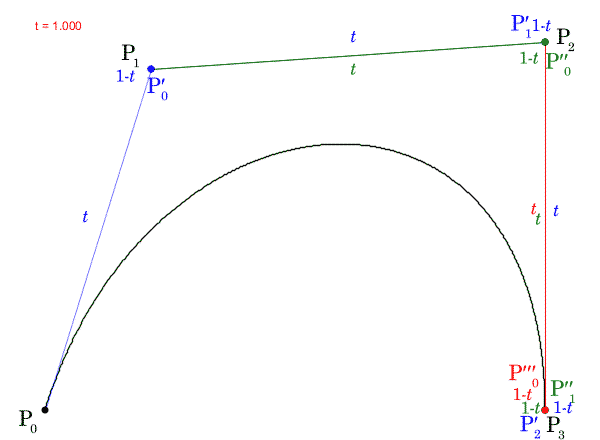
この の座標
は、次の式で与えられます。ただし
は制御点の座標を示すベクタです。
N次ベジェ
N次のベジェ曲線はN+1個の制御点の列 で定義されます。
2次, 3次の時と同様に、隣り合う制御点を結ぶ線分を内分して点を求め、それを点が一つになるまで繰り返していくという操作によりベジェ曲線上の点を求めることができます。
また、パラメータ に対応するベジェ曲線上の点
は次式で定義されます。
ただし、 は次の式で定義され、n次のバーンスタイン基底関数とよばれます。
他の方法
ド・カステリョのアルゴリズムを使って1つのベジェ曲線を2つのベジェ曲線に分割することができるので、それを利用して曲線を再帰的に分割していって求める曲線を計算するということもできるのですが、実際に手描きで分割して曲線上の点を求めていくとすぐに線が込み入ってよく分からなくなる感じがあります。
参考
- コンピュータグラフィックス編集委員会『コンピュータグラフィックス』, CG-ARTS協会, 2004
- 最近新版が出ました。そちらをおすすめします。
*1:TrueTypeフォントは2次B-スプラインらしいですが、TrueTypeフォントの制御点列で連続するoff-curve点の中点にon-curve点を挿入すると、2次ベジェ曲線の集まりと考えられます。


