にせねこメモ

はてなダイアリーがUTF-8じゃないので移ってきました。

Wordファイル公開にあたって、個人情報メタデータを消す

Microsoft Word (.docx)ファイルには本文以外にも、作成者名やファイルパス等の個人情報がメタデータとして含まれている可能性がある。

公開前に消しときたいというのはある。

ついでにExcelやPower Pointなどの他のMicrosoft Officeファイルでも同様である。

方法A: Windowsエクスプローラーを使って作成者名等を消す

  1. WindowsのエクスプローラーからWordファイルを右クリック→[プロパティ(R)]
  2. [詳細]タブ→[プロパティや個人情報を削除]をクリック
  3. 必要な設定を変更するなどして、[OK]を押す

参考: Word , Excel , PowerPoint のタイトルや作成者などプロパティ情報を変更または削除する方法。 | PC＆IT ～i-TSUNAGU～

方法B: Wordから削除・編集する

Wordのバージョンは「Microsoft® Word for Microsoft 365 MSO (バージョン 2112 ビルド 16.0.14729.20156) 64 ビット」である。

[ファイル]→[情報]を開くと、右側に[関連ユーザー]のところに[作成者]と[最終更新者]が表示されている。

[作成者]についてはこのユーザーを右クリックして削除や変更ができるが、[最終更新者]については変更ができない用に見える。

これらを消すためには、

  1. [ファイル]→[情報]→[問題のチェック]([文書の検査]の左)をクリック→[ドキュメント検査(I)]をクリック
  2. [ドキュメントのプロパティと個人情報(U)]にチェックが入っていることを確認し、[検査(I)]をクリック
  3. [ドキュメントのプロパティと個人情報]の右側に表示される[すべて削除]をクリック→[閉じる(C)]をクリックして閉じる
  4. ファイルを保存する

このような手順でできる。

参考: Wordのファイルで、自分ではない作成者名が表示されてしまうのですが? | 日経クロステック（xTECH）

方法C: .docxファイルを直接いじる

.docxファイルがXMLファイル等を.zip圧縮したものであるというのは周知の通りである。

なので、展開して内部のXMLファイルを変更し、再度圧縮して.docxという拡張子に戻すことで変更できる。
テキストファイルなので全文検索を通しておくと安心だと思う。


今回自分が編集していたWordファイルでは、

  • docProps/core.xmlのdc:creator, cp:lastModifiedByタグに作者の名前が出るっぽかったので、書き換えると良さそう。

あと、差し込み文書用データのExcelファイルのパスが

  • word/_rels/settings.xml.rels
  • word/settings.xml

に含まれていたので、ファイルの場所を個人情報を含まないものに変更しておくなどするとよいかもしれない。

Online Armenian Storeで買物しようとしたら日本へは送れないよと言われた

語学

アルメニア語の辞書が欲しくて探していたところ、Online Armenian Storeというアルメニアの物品を売っているサイトを見つけた。
onlinearmenianstore.com
商品名が英語で書かれているので、検索も楽だし、アルメニア語わからなくてもだいたいどんな本かわかるので便利そうだ。

しかし、ここで買おうとしたら、お前のアドレスには配送できないよというエラーが表示された。

This order can’t be shipped to the address you entered. Review your address to ensure that all fields have been entered correctly and try again.
配送方法がない

さて、問題の商品を見てみると、Shipped from USと書いてある。

商品ページにShipped from USと書いてある
Shipped from USと書いてある商品

一方で、検索してみると、Shipped from Armeniaと書かれている商品もある。

商品ページにShipped from Armeniaと書いてある
Shipped from Armeniaと書いてある商品

ここで、サイトの最下部に

Worldwide Shipping
We ship from Armenia using Haypost and Onex. ...

と書いてあることを考えると、どうやらアメリカから発送するのは日本まで送ってくれなさそうだ。

というわけで、カートからShipped from USと書かれた商品をすべて削除したら送料選択の画面に進むことができた。送料も安いし便利そうだ。

配送

アルメニアから国際書留で送られてきた。注文から届くまで3週間ちょっとかかった。2週間以内では確実に届かないだろうので、気長に待つのがよいかもしれない。

f:id:nixeneko:20220102174241j:plain
届いた辞書

Windows用入力言語切り替えボタンを作る

AutoHotKey 語学

概要

youtu.be

キーパッドとAutoHotkeyスクリプトを組み合わせることでキーボードレイアウトを切り替える仕組みを作った。
F13-F24のキーを使用することで、キーボードの既存のキーを犠牲にすることなく実現ができた。

あいさつ

この記事は「語学・言語学・言語創作 Advent Calendar 2021」の13日目として書かれています。

語学・多言語学習畑から乱入失礼します。なんかconlang系の人が多そうですが、混乱させてしまったらすみません。


……。

はじめに

さて、多言語をかじったりしていると、いろいろな言語を入力する必要があります。
Windowsで多言語入力をするには、キーボードレイアウトを言語ごとに追加し、切り替えて入力することが多いと思います。（以下ではキーボードレイアウトは単に「キーボード」と書き、物理的なキーボードは「物理キーボード」と書いて区別することとします。）

この切り替えは言語ごとに順繰りに送っていく方式で、2～3個ならまだ切り替えるのは問題ないのですが、5個以上になってくると、目的のキーボードまで切り替えるのがかなり面倒になります。別の言語に切り替えるためにAlt+Shiftを5連打とかしないといけないのはあんまりうれしくないわけです。
ラテン文字系であれば、WinComposeなどの汎言語的に入力できるツールを使えばキーボードを切り替えなくてもよいものの、非ラテン文字の場合は使うことはできません。

そのため、キーボードを、つまり実質的には入力言語*1を切り替えることができる専用のボタンがあれば便利なのではないでしょうか。

前に検討した仕組みの問題点

私は以前にAutoHotkeyを利用してキーボードを切り替える仕組みを検討していました。

しかし、これは物理キーボードのキーを横取りしているため、使用したキーが入力できなくなってしまうという副作用が生じます。

これについては、「Windowsが認識できるが、普通のキーボードには存在しないキーコード」を出力する物理キーボード（キーパッド）を用意すれば解決します。具体的にはF13～F24というキーコードが存在していて、Windowsが認識できるようになっているので、これを使うことにしました。

キーパッド: meishi2

f:id:nixeneko:20211212200801p:plain
自分で適当なキーコードを設定できるキーパッドを用意します。キーパッドはマクロパッドとも呼ばれ、要するに「自由にキーを設定できる、キーの少ないキーボード」のことです。今回はmeishi2というキーボードキットを使いました。

キーの割当ですが、左からF13, F14, F15, F16としました。また、4言語では足りないのでは？と思い、2キーの同時押しに対してもF17～F22を割り当てています。


キーの割り当てを設定するために、QMK Firmwareをビルドして書き込むみました。

QMK Firmwareのビルドについては特に解説しませんが、次のページを参考にしています。

qmk_firmware\keyboards\meishi2\keymaps\lang_selector以下に次のキーマップのファイルをコピーし、

make meishi2:default:avrdudeとかするといいです。

AutoHotkeyスクリプト

github.com
作成したAutoHotkeyスクリプトをここに置きました。

使用準備

  1. F13-F24のキーをもつキーパッドを繋ぎます。
  2. AutoHotkey v1.1をインストールします。
  3. change_settings.ahkを起動します。
  4. 現在のキーボードを、キーに割り付けたいキーボードに変更します。
  5. キーパッドのF13-F24のいずれかのキーを押します。するとそのキーに現在のキーボードが割り付けられ、その旨を示すダイアログが表示されるのでOKを押して閉じます。settings.iniが更新されます。
  6. 他にキーボードがあれば 4. に戻ります。
  7. 通知領域のAutoHotkeyのアイコンを右クリックし、Exitを選んで終了します。

キーボードの切り替え

  1. keyboard_changer.ahkを起動します。
  2. F13-F24のキーを押すと、先に設定したキーボードに切り替わります。

制限

現在は「キーボードの切り替え」であり、IMEの切り替えには対応していません。そのため、「Google日本語入力」と「Microsoft 日本語 IME」を切り替えるみたいなことができません。これはIMEはTSFという枠組みで動いているので、キーボード自体は同じものを指していて、キーボード切り替えの仕組みでは区別ができないためです。
これについてはTSF系のAPIを叩くことでなんとかできそうな気はします。

また、IMEのオン・オフを指定して切り替える仕組みも作ったのですが、利用したIME.ahkのライセンスが不明なので省いてあります。
詳しくはkeyboard_changer.ahkのソースを見てもらえばよいのですが、IME.ahkをダウンロードしてきてIME_SET関数をコピペし、関連するコメントアウトを外し、settings.iniを適切に設定すると動くようにはなります。

おわりに

多言語入力においてキーボードの切り替えが面倒だったために、Windowsに同時に設定するキーボードの数を3個程度に制限していたのですが、これで遠慮なく増やせます。現在の状態を意識しなくても目的の言語に切り替えられるのは便利です。

みなさんも素敵な多言語入力ライフをお過ごしください。

.i mi do ckire lo nu tcidu kei .i co'o rodo
.i lo lenku tcima cu ba ranji .i ko ko kurji

2021-12-13 15:45追記

こんだけ書いといてなんですが、Windowsで入力言語に対してショートカットキーが設定できました。
以前ショートカットキー設定したときは設定が反映されなかったので検討しなかったのですが、動くようになっていたのですね。

Windowsの設定→「デバイス」→「入力」→「キーボードの詳細設定」→「入力言語のホットキー」
で出てくるウィンドウで目的のキーボードに対してキーシーケンスを設定すればいいようです。

設定したキーシーケンスを出力するキーボードを用意すればAutoHotkeyスクリプト要らなかったですね。
まあショートカットキーが設定できるキーシーケンスは限られているため、ショートカットキーが被る可能性はあり、ショートカットキーの競合が少なくなるという点でAutoHotkeyを使う優位性はあるかもしれません。

*1:一つの言語に対して複数のキーボードを使うことは少ないと思ってこう書いていますが、一言語を複数の用字系で表記する場合などに同じ言語の複数のキーボードを使う必要が生じたりします。

Windows 10でWacomのタブレットを使うと手書き入力パネルが出てきて困る

Windows

まとめ

タブレットの設定からWindows Ink機能を使わないように設定する

問題

  • Windows 10でWacomのタブレット(CTH-661)を使っている
  • ペンでテキスト入力欄にタッチすると手書き入力用のパネルが現れる
    • これを消したい(キーボードは別に接続してあるため不要なので)

解決策

製品等によって異なるが、Windows Ink機能を利用しない様に設定するとよい。
次の説明はCTH-661のためのもの。

  1. Windowsのスタートメニューから「ワコム」→「ワコムの設定」を開く
  2. 「ペン」タブを開く
  3. 「座標検出モード」の「ペンモード」のところの「マッピング...」ボタンをクリック
  4. 「デジタルインクを使う」のチェックボックスを外して「OK」を押す

その他

手書き入力パネルを無効にしたいと検索すると「Touch Keyboard and Handwriting Panel Service」を無効にすればよいと説明しているページが出てくるが、このサービスを無効にすると問題が発生する。

その名前に反してテキスト入力に結構深くかかわっているらしく、無効にすると日本語入力ができなくなる。

NextDNSを使って深夜にTwitterにアクセスできないようにする

ツール

NextDNSを使って、特定の時間帯のみTwitterにアクセスできるように設定した。

モチベーション

深夜延々とツイッターを見てしまうということがある。人によってはTwitterでなくてYouTubeとかかもしれない。これをアクセス不可能にできればゆっくり眠れるのかなあと思うこともある。

特定の時間帯にアクセス不能にするというのは、DNSをカスタマイズすればできる。ただ、自分でDNSサーバーを立てるのは面倒だし、家のLAN/Wifi環境とそれ以外で統一的に利用できるようにするのは大変*1なので、なかなか難しい。

NextDNS

NextDNSというDNSサービスがあり、これは簡単にいうと自分で好きにカスタマイズできるDNSである。

この設定項目の中に「ペアレンタルコントロール」というものがあり、特定のサイトへのアクセスを制限でき、「娯楽時間」の設定で、接続を許可する時間を設定できる。

つまり、深夜帯以外を「娯楽時間」に設定することで、深夜はTwitterにアクセス不可にすることが可能だ。
また、システム全体に設定することで、家の中でも外でも同じDNSを使うことができる。

NextDNSは無料で30万クエリ/月まで利用でき、制限のないProプランだと250円/月となる。
まずは登録なしで一週間利用できるので試してみるといいのかもしれない。

以下、試してみたことと、感想を書いていく。

設定方法

NextDNSのトップページを開き、“Try it now”ボタンをクリックするといきなりDNSサービスが準備される。
これをデバイスに設定すると利用準備が完了する。

DNSの端末への設定

NextDNSの設定ページの「セットアップガイド」に従って準備する。

  • Windowsでは設定用のソフトをインストールして使用するか、自分で設定を変更するかのどちらかの方法があるらしい。
  • Androidでは「プライベート DNS」で設定するのが便利らしい。
  • ルーターに設定してもいいが、それに接続する端末すべてに影響しうるので、他にそのルータを使用して接続するすべての人の了解を得てからやった方がよい。自分だけが利用するルータを用意するというのも手ではある。

ペアレンタルコントロールの設定

「ペアレンタルコントロール」タブを開き、「ウェブサイト、アプリ、ゲーム」セクションで、アクセスを制限したいWebサイトやアプリを追加する。

「娯楽時間」セクションで時間を設定する。

f:id:nixeneko:20211007134855p:plain
娯楽時間の設定例

30分刻みでしか設定できないのと、終端の時間が23:30までしか設定できない、また複数時間帯を設定できないのが不便っぽい。

「ウェブサイト、アプリ、ゲーム」セクションで、設定したい項目の右の方にあるグレーの時計マーク🕓をクリックして有効化する。有効にすると緑色になる。

f:id:nixeneko:20211007135036p:plain
娯楽時間の有効化

設定の永続化

このままだと7日間で期限切れとなってまうので、継続して使用したければ登録する必要がある。
設定ページの上の「新規登録」ボタンを押すと登録画面に進むので、メールアドレスとパスワードを設定すればアカウントが作成される。

本当に効くのか？

さて、DNSによる名前解決の結果は端末にキャッシュされる。
そのため、アクセス制限しても、それまでに通信していた場合にしばらくは繋がることになるかもしれない。

実際にAndroid端末でやってみると、しばらくはTwitterは普通に読み込みできる。10分ほどすると、TwitterのWebサイトにつながらなくなる一方、アプリでは次第に（キャッシュされてない）画像等が表示されなくなるもののテキスト情報の読み込みはできる。1時間ほどして確認してみたらアプリで新しいツイートが読み込めなくなっていた。
もう一度やってみたら遮断開始時刻から1分ほどで画像が読み込めなくなり、10分程度で完全に読み込めなくなった。

YouTubeアプリでやってみたら、制限して5分ほどしたら新しく再生を開始した動画の再生が止まるようになった。

というわけで、時間差はあるがそのうち効いてくるという感じっぽい。なるほど。

課題点

  • リストにないサイト・アプリはペアレンタルコントロールに追加できるのか？
  • ペアレンタルコントロールの時間をもっと細かく設定できないか？
    • 6:00-10:00, 15:00-21:00とか、0:00-1:00, 5:00-24:00とかね…
    • 日を跨げないの厳しい
  • ルータで設定したDNSルーティング設定が使えない（それはそう）
  • 30万クエリ/月というのは心もとない。Android端末一つだけでも1000クエリ/時程度は行くので、複数端末使えば簡単に突破するのでは？
    • まともに使いたければ課金が必要そう。高くはないが…

感想

全体としては良い感じだと思うし、有用なケースはある。ただ、ペアレンタルコントロールの設定があまり柔軟でなく、もっと改善の余地があるなあと思った。

参考

nextdnsがペアレンタルコントロールにすごく良かった - Qiita

*1:これはLAN内でDNSサーバを動かした場合で、対策としてはVPSとか借りればいいわけですが、そこにそんなに金かけたくないし…

1次B-スプライン曲線の制御点列をそのまま利用して2次B-スプライン曲線で1次B-スプライン曲線を近似する

画像処理 TrueType

問題提起

1次B-スプライン曲線(linear B-spline curve)とはすなわち折れ線のことである。
これはシンプルで、隣り合う2制御点を順番に直線で結んでいけば求める曲線(というか折れ線)が描ける。

一方で、2次B-スプライン曲線(quadratic B-spline curve)はB-スプライン基底関数という2次関数を使って制御点の影響を計算して曲線を描く。
基本的に2次B-スプライン曲線では、連続する制御点を結んだ折れ線、つまり直線の連続を描くことができない。
1次B-スプライン曲線の隣り合う2制御点の中点*1を制御点として2点間に挿入し、ノットベクトル(後述)を[0, 0, 0, 1, 1, 2, 2, 3, 3, 4, 4, 4]みたいにすると直線が表現できるが、制御点列としては別のものになる。


さて、ここで、1次B-スプライン曲線の制御点列をそのまま利用して、2次B-スプライン曲線で1次B-スプライン曲線を表現することはできるだろうか？

モチベーション

TrueTypeアウトラインの曲線部分は2次B-スプライン曲線の特殊な場合であるが、2次B-スプライン曲線は隣り合う2制御点を結ぶような折れ線、つまり1次B-スプライン曲線はふつう表現できない。そのため、TrueTypeアウトラインのcontourの制御点と2次B-スプライン曲線の制御点は同一ではないと考えていた。

一方で、もしそのような折れ線を2次B-スプラインで表現できるのであれば、直線部分も2次B-スプライン曲線として表現可能になり、任意のTrueTypeアウトラインは制御点を挿入することなしに2次B-スプライン曲線だと言えるのではないかと思う。

B-スプライン曲線の定義

n次のB-スプライン曲線とは、制御点列(control points) \{\boldsymbol P_i\}とノットベクトル(knot vector) \{ t_i \}で定義される曲線である。曲線の補間(制御点の影響の計算)にはn次のB-スプライン基底関数が用いられる。

n次のB-スプライン基底関数(n-th order B-spline basis function) N_i^n(t)は、次のように定義される。(コンピュータグラフィックス編集委員会(2004), p.66 (3.29)式)
\displaystyle N_i^0(t) = \left\{ \begin{array}{ll} 1 & (\text{if} \quad t_i \leq t < t_{i+1}) \\ 0 & (\text{if} \quad t_i \leq t < t_{i+1}) \end{array} \right.

\displaystyle N_i^n(t) = \frac{t-t_i}{t_{i+n}-t_{i}} N_i^{n-1}(t) + \frac{t_{i+n+1}-t}{t_{i+n+1}-t_{i+1}} N_{i+1}^{n-1}(t) \quad (n\geq 1)

これを使って、L個のセグメントからなるn次B-スプライン曲線は次のように定義される。
\displaystyle \boldsymbol{P}(t) = \sum_{i=0}^{n+L-1}\boldsymbol{P}_iN_i^n(t) \quad (t_n \leq t < t_{n+L})

1次B-スプライン曲線

さてここで、1次B-スプライン曲線の場合を見ていく。

L個のセグメントからなる1次B-スプライン曲線は次のように定義される。
\displaystyle \boldsymbol{P}(t) = \sum_{i=0}^{L}\boldsymbol{P}_iN_i^1(t) \quad (t_1 \leq t < t_{L+1})

ここで、 0 \leq k < Lなる整数 kに関して、点 \boldsymbol{P}_kと \boldsymbol{P}_{k+1}で定義される一つのセグメント ( t_{k+1} \leq t < t_{k+2})だけをみると、
\displaystyle \boldsymbol{P}(t) = \boldsymbol{P}_kN_k^1(t) + \boldsymbol{P}_{k+1}N_{k+1}^1(t)

ここで、B-スプライン基底関数は次のようになる。
\displaystyle N_k^0(t) = 0

\displaystyle N_{k+1}^0(t) = 1

\displaystyle N_{k+2}^0(t) = 0

\displaystyle \begin{eqnarray*} N_k^1(t) &=& \frac{t-t_k}{t_{k+1}-t_k} N_k^0(t) + \frac{t_{k+2}-t}{t_{k+2}-t_{k+1}} N_{k+1}^0(t) \\ &=& \frac{t-t_k}{t_{k+1}-t_k} \cdot 0 + \frac{t_{k+2}-t}{t_{k+2}-t_{k+1}} \cdot 1 \\ &=& \frac{t_{k+2}-t}{t_{k+2}-t_{k+1}} \end{eqnarray*}

\displaystyle \begin{eqnarray*} N_{k+1}^1(t) &=& \frac{t-t_{k+1}}{t_{k+2}-t_{k+1}} N_{k+1}^0(t) + \frac{t_{k+3}-t}{t_{k+3}-t_{k+2}} N_{k+2}^0(t) \\ &=& \frac{t-t_{k+1}}{t_{k+2}-t_{k+1}} \cdot 1 + \frac{t_{k+3}-t}{t_{k+3}-t_{k+2}} \cdot 0 \\ &=& \frac{t-t_{k+1}}{t_{k+2}-t_{k+1}} \end{eqnarray*}

したがって、
\displaystyle \boldsymbol{P}(t) = \frac{t_{k+2}-t}{t_{k+2}-t_{k+1}}\boldsymbol{P}_k + \frac{t-t_{k+1}}{t_{k+2}-t_{k+1}}\boldsymbol{P}_{k+1}
というわけで2点間の線形補間になっている=直線であることがわかる。

2次B-スプライン曲線

さて、次に2次B-スプライン曲線の場合について考える。

2次B-スプライン曲線の1つのセグメントは3点の制御点からなる。そのため、1次B-スプライン曲線と同じ数のセグメントを用意するためには、制御点を最後に一個追加しないといけない。

L個のセグメントからなる2次B-スプライン曲線は次のように定義される。
\displaystyle \boldsymbol{P}(t) = \sum_{i=0}^{L+1}\boldsymbol{P}_iN_i^2(t) \quad (t_2 \leq t < t_{L+2})

ここで、 0 \leq k < Lなる整数 kについて、点 \boldsymbol{P}_kと \boldsymbol{P}_{k+1}, \boldsymbol{P}_{k+2}で定義される一つのセグメント t_{k+2} \leq t < t_{k+3}だけをみると、

\displaystyle \boldsymbol{P}(t) = \boldsymbol{P}_kN_k^2(t) + \boldsymbol{P}_{k+1}N_{k+1}^2(t) + \boldsymbol{P}_{k+2}N_{k+2}^2(t)
となる。

1次B-スプライン曲線の近似

さて、ここでノットベクトルとして次のような公比を無限大に近づけた等比数列 \{ t_i \}を考える*2。
\displaystyle t_i = \lim_{r \to +\infty} ar^{i} ただし \displaystyle a>0

すると、 \displaystyle t_{k+2} \leq t < t_{k+3}において、B-スプライン基底関数は次のように計算される。

後の計算で必要となるもの

\displaystyle \frac{t_{k+2}}{t_{k+3}} = \lim_{r \to +\infty}\frac{1}{r} = 0

\displaystyle \frac{t_{k+3}}{t_{k+4}} = \lim_{r \to +\infty}\frac{1}{r} = 0

\displaystyle \frac{t_{k+2}}{t_{k+4}} = \lim_{r \to +\infty}\frac{1}{r^2} = 0

\displaystyle \frac{t_{k+2}}{t_{k+4}} \leq \frac{t}{t_{k+4}} < \frac{t_{k+3}}{t_{k+4}} \quad (\because t_{k+2} \leq t < t_{k+3})より \displaystyle \frac{t}{t_{k+4}} = 0

0次

\displaystyle N_k^0(t) = 0

\displaystyle N_{k+1}^0(t) = 0

\displaystyle N_{k+2}^0(t) = 1

\displaystyle N_{k+3}^0(t) = 0

\displaystyle N_{k+4}^0(t) = 0

1次

\displaystyle \begin{eqnarray*} N_k^1(t) &=& \frac{t-t_k}{t_{k+1}-t_k} N_k^0(t) + \frac{t_{k+2}-t}{t_{k+2}-t_{k+1}} N_{k+1}^0(t) \\ &=& \frac{t-t_k}{t_{k+1}-t_k} \cdot 0 + \frac{t_{k+2}-t}{t_{k+2}-t_{k+1}} \cdot 0 = 0 \end{eqnarray*}

\displaystyle \begin{eqnarray*} N_{k+1}^1(t) &=& \frac{t-t_{k+1}}{t_{k+2}-t_{k+1}} N_{k+1}^0(t) + \frac{t_{k+3}-t}{t_{k+3}-t_{k+2}} N_{k+2}^0(t) \\ &=& \frac{t-t_{k+1}}{t_{k+2}-t_{k+1}} \cdot 0 + \frac{t_{k+3}-t}{t_{k+3}-t_{k+2}} \cdot 1 = \frac{t_{k+3}-t}{t_{k+3}-t_{k+2}} \end{eqnarray*}

\displaystyle \begin{eqnarray*} N_{k+2}^1(t) &=& \frac{t-t_{k+2}}{t_{k+3}-t_{k+2}} N_{k+2}^0(t) + \frac{t_{k+4}-t}{t_{k+4}-t_{k+3}} N_{k+3}^0(t) \\ &=& \frac{t-t_{k+2}}{t_{k+3}-t_{k+2}} \cdot 1 + \frac{t_{k+4}-t}{t_{k+4}-t_{k+3}} \cdot 0 = \frac{t-t_{k+2}}{t_{k+3}-t_{k+2}} \end{eqnarray*}

\displaystyle \begin{eqnarray*} N_{k+3}^1(t) &=& \frac{t-t_{k+3}}{t_{k+4}-t_{k+3}} N_{k+3}^0(t) + \frac{t_{k+5}-t}{t_{k+5}-t_{k+4}} N_{k+4}^0(t) \\ &=& \frac{t-t_{k+3}}{t_{k+4}-t_{k+3}} \cdot 0 + \frac{t_{k+5}-t}{t_{k+5}-t_{k+4}} \cdot 0 = 0 \end{eqnarray*}

2次

\displaystyle \begin{eqnarray*} N_k^2(t) &=& \frac{t-t_k}{t_{k+2}-t_k} N_k^1(t) + \frac{t_{k+3}-t}{t_{k+3}-t_{k+1}} N_{k+1}^1(t) \\ &=& \frac{t-t_k}{t_{k+2}-t_k} \cdot 0 + \frac{t_{k+3}-t}{t_{k+3}-t_{k+1}} \cdot \frac{t_{k+3}-t}{t_{k+3}-t_{k+2}} \\ &=& \frac{t_{k+3}-t}{t_{k+3}-t_{k+1}} \cdot \frac{t_{k+3}-t}{t_{k+3}-t_{k+2}} \\ &=& \frac{1-\frac{t}{t_{k+3}}}{1-\frac{t_{k+1}}{t_{k+3}}} \cdot \frac{1-\frac{t}{t_{k+3}}}{1-\frac{t_{k+2}}{t_{k+3}}} \\ &=& \left(1-\frac{t}{t_{k+3}}\right)^2 \end{eqnarray*}

\displaystyle \begin{eqnarray*} N_{k+1}^2(t) &=& \frac{t-t_{k+1}}{t_{k+3}-t_{k+1}} N_{k+1}^1(t) + \frac{t_{k+4}-t}{t_{k+4}-t_{k+2}} N_{k+2}^1(t) \\ &=& \frac{t-t_{k+1}}{t_{k+3}-t_{k+1}} \cdot \frac{t_{k+3}-t}{t_{k+3}-t_{k+2}} + \frac{t_{k+4}-t}{t_{k+4}-t_{k+2}} \cdot \frac{t-t_{k+2}}{t_{k+3}-t_{k+2}} \end{eqnarray*}

\displaystyle \begin{eqnarray*} \frac{t-t_{k+1}}{t_{k+3}-t_{k+1}} \cdot \frac{t_{k+3}-t}{t_{k+3}-t_{k+2}} &=& \frac{\frac{t}{t_{k+3}}-\frac{t_{k+1}}{t_{k+3}}}{1-\frac{t_{k+1}}{t_{k+3}}} \cdot \frac{1-\frac{t}{t_{k+3}}}{1-\frac{t_{k+2}}{t_{k+3}}} \\ &=& \frac{t}{t_{k+3}} \left( 1-\frac{t}{t_{k+3}} \right) \end{eqnarray*}

\displaystyle \begin{eqnarray*} \frac{t_{k+4}-t}{t_{k+4}-t_{k+2}} \cdot \frac{t-t_{k+2}}{t_{k+3}-t_{k+2}} &=& \frac{1-\frac{t}{t_{k+4}}}{1-\frac{t_{k+2}}{t_{k+4}}} \cdot \frac{\frac{t}{t_{k+3}}-\frac{t_{k+2}}{t_{k+3}}}{1-\frac{t_{k+2}}{t_{k+3}}} \\ &=& \left( 1-\frac{t}{t_{k+4}}\right) \cdot \frac{t}{t_{k+3}} = \frac{t}{t_{k+3}} \end{eqnarray*}
よって
\displaystyle \begin{eqnarray*} N_{k+1}^2(t) &=& \frac{t}{t_{k+3}} \left( 1-\frac{t}{t_{k+3}} \right) + \frac{t}{t_{k+3}} \\ &=& \frac{t}{t_{k+3}} \left( 2-\frac{t}{t_{k+3}} \right) \end{eqnarray*}

また、
\displaystyle \begin{eqnarray*} N_{k+2}^2(t) &=& \frac{t-t_{k+2}}{t_{k+4}-t_{k+2}} N_{k+2}^1(t) + \frac{t_{k+5}-t}{t_{k+5}-t_{k+3}} N_{k+3}^1(t) \\ &=& \frac{t-t_{k+2}}{t_{k+4}-t_{k+2}} \cdot \frac{t-t_{k+2}}{t_{k+3}-t_{k+2}} + \frac{t_{k+5}-t}{t_{k+5}-t_{k+3}} \cdot 0 \\ &=& \frac{t-t_{k+2}}{t_{k+4}-t_{k+2}} \cdot \frac{t-t_{k+2}}{t_{k+3}-t_{k+2}} \\ &=& \frac{\frac{t}{t_{k+4}}-\frac{t_{k+2}}{t_{k+4}}}{1-\frac{t_{k+2}}{t_{k+4}}} \cdot \frac{\frac{t}{t_{k+3}}-\frac{t_{k+2}}{t_{k+3}}}{1-\frac{t_{k+2}}{t_{k+3}}} \\ &=& \frac{t}{t_{k+4}} \cdot \frac{t}{t_{k+3}} = 0 \cdot \frac{t}{t_{k+3}} = 0 \end{eqnarray*}


ここから、 \displaystyle N_{k+2}^2(t) = 0なので \boldsymbol P_{k+2}の関与が完全になくなっていることがわかる。

また、 \displaystyle N_{k}^2(t) + N_{k+1}^2(t) = 1となることもわかる。

y = \displaystyle N_{k}^2(t), y = \displaystyle N_{k+1}^2(t)のグラフを描くとだいたい次のような感じになる*3。
f:id:nixeneko:20210814154404j:plain

実際に描いてみた

プログラムを使って描いてみた。さすがに無限大は扱えないので適当に大きな値にしてみる。

描画に用いたPython3コードを次に示す*4。STEPが公比rに相当する。
gist.github.com

描画結果

赤が正解となる1次B-スプライン曲線、黒が2次B-スプライン曲線である。

r=10

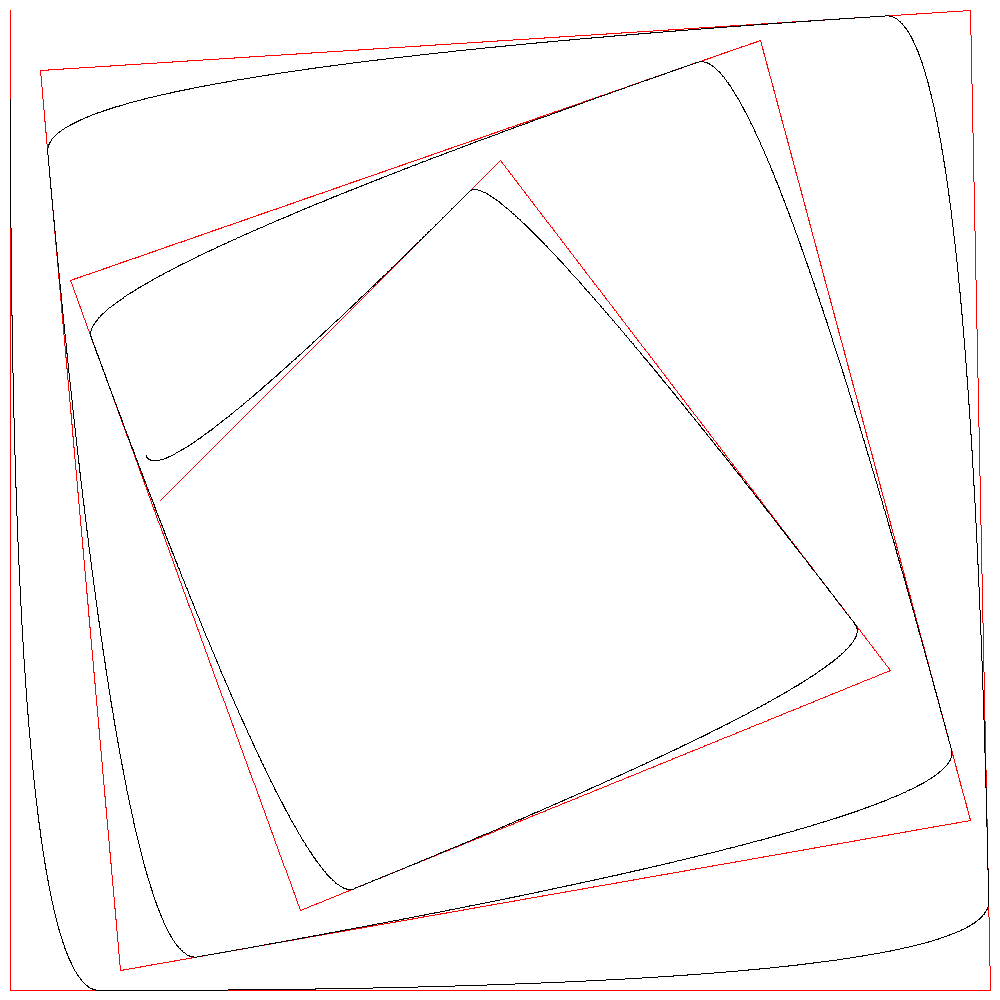
f:id:nixeneko:20210813092559p:plain

r=100

f:id:nixeneko:20210813092614p:plain

r=1000

f:id:nixeneko:20210813092622p:plain

r=10000

f:id:nixeneko:20210813092638p:plain
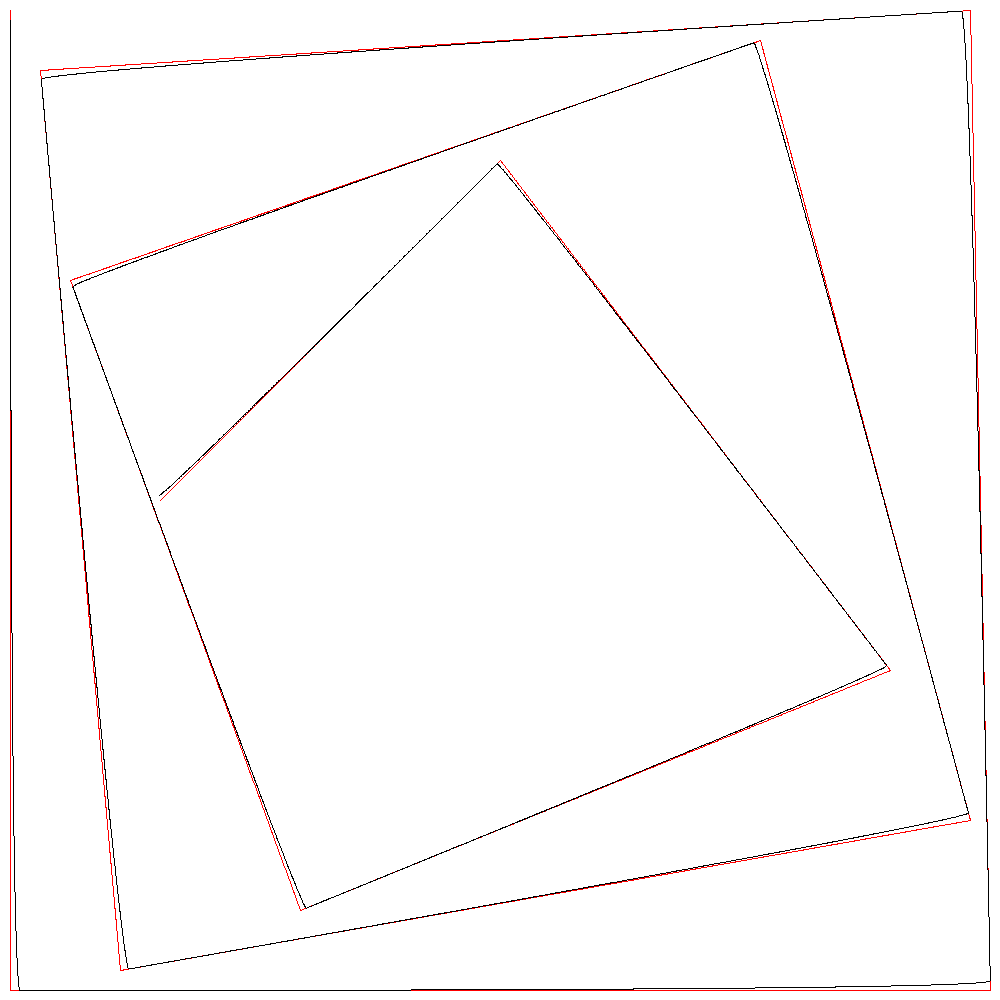
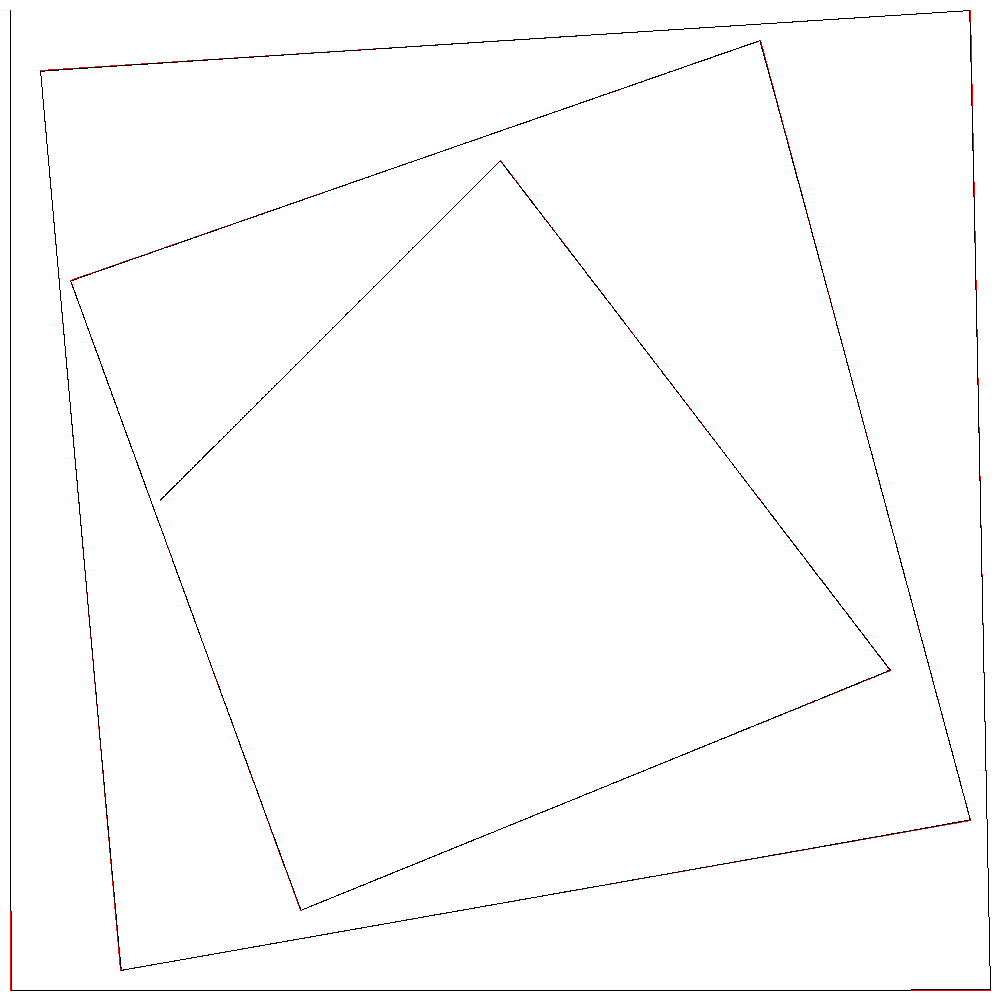
r=10000でほぼ一致している。
隣り合う2制御点をr:1で内分する点を通る曲線が描かれているので、r=10000のときは2点を10000:1に内分する点を通る曲線となる。誤差が1ピクセルより小さくなるので直線に見えるというわけである。
画像サイズが(1000, 1000)なので公比r=10000程度でも直線になっているが、ドローソフトで線を拡大していく場合などはそれでも足りなくなると思う。
r=10000の場合、制御点15個に対して最初のノット値と最後のノット値を比べると1064倍になっている。複雑な図形にしたらすぐにあふれそう。

考察

1次B-スプライン曲線を(制御点を変更せずに)2次B-スプライン曲線を使って表現できる(そのようなノットベクトルの取り方が存在する)ことがわかった。

つまり、適切にノットベクトルを用意すれば、TrueTypeアウトラインのcontourをそのまま2次B-スプラインを用いて描画可能なのでは？

というわけで試してみる。
用意するのは次の制御点列。onはTrueTypeにおけるon-curve点、offはoff-curve点を示す。

idx 座標 on/off
0 (10, 10) on
1 (10, 990) on
2 (250, 500) off
3 (500, 990) off
4 (750, 500) off
5 (990, 990) on
6 (990, 10) on
7 (500, 500) off
8 (10, 10) on

これに対して、
\displaystyle \boldsymbol t = \lim_{r \to +\infty}\{r^0, r^0, r^0, r^1, r^2, 2r^2, 3r^2, 4r^2, r^3, r^4, r^4, r^4\}
みたいなノットベクトルを用意してみたらどうだろう。


r=10000として計算したのが次の画像である。この手法で計算された曲線が黒い線となっている。
f:id:nixeneko:20210814200729p:plain
制御点を青の点で示している。制御点列を結んだ直線が水色の直線である。
赤は正解となる2次B-スプライン曲線で、2連続するon-curve点の途中にその2点の中点をoff-curveな制御点として挿入してon-curve点の連続をなくし、ノットベクトルを[0, 0, 0, 1, 1, 2, 3, 4, 4, 5, 5, 6, 6, 6]としたものであるが、黒い線の下に入ってほぼ見えなくなっている。

描画に使用したPython3コードは次のものである。


というわけで、こんな感じのわけわからんノットベクトルを用意すれば、同一の制御点列を用いつつも2次B-スプライン曲線はTrueTypeアウトラインのcontourに一致する気がする*5。
ちゃんと計算すれば(上でやったのと同じような議論で)示せると思うけど面倒なので気になったら各自計算してね…

感想

無限大を導入すれば、任意のTrueTypeアウトラインのcontourの制御点列をそのまま2次B-スプライン曲線の制御点列として、同一のアウトラインを描けるノットベクトルの取り方が存在しそう、ということがわかった。無限大を導入すれば……

コンピュータで扱う数値計算に無限大を導入するな💢

実用としては素直に直線で計算するべし。

参考書籍

*1:別に内分点であればいいけど

*2:こういう数式の書き方で正しいのかわからないけど、とにかく公比をめちゃくちゃ大きくした等比数列だと思ってください。

*3:ガタガタしてるように見えるのは描くのが下手なだけので気にしないで…。普通の放物線です。

*4:このコード、めちゃくちゃ効率が悪いしあんまり汎用性もないです。あしからず。

*5:最後が直線になる場合はノット重ねるとベジエになっちゃうのでダミーの制御点追加しないといけないけど、一様B-スプライン曲線の描画と同様に制御点ループさせればいいので問題ないか…。

Pleromaのホームタイムラインが500エラー返すようになってた

Pleroma

PostgreSQLの実行でタイムアウトしていたので、VACUUM ANALYZEを実行したら解決した。

問題

以前Pleromaのサーバを移行したが、

その後、多少問題はあったが普通に動いていた。

環境はPleroma 2.3.0で、ソースからインストールしたものである。


しかし、今日急に、SubwayTooterでホームタイムラインを取得しようとした(GET /api/v1/timelines/home)場合に、500 Internal Server Errorが返ってくるようになった。(ブラウザからは普通に見れていたのでよくわからない…)

さてどうしたものか。

調査

サーバーにログインし、

sudo journalctl -fu pleroma.service

実行する。するとpleromaのログが流れてくる。

ここでSubwayTooterでホームタイムラインを取得しようとすると、次のようなログがでてくる。時刻やrequest_idなど先頭部分は省いている。

[info] GET /api/v1/timelines/home
[error] Postgrex.Protocol (#PID<■■■>) disconnected: ** (DBConnection.ConnectionError) client #PID<■■■> timed out because it queued and checked out the connection for longer than 15000ms
#PID<■■■> was at location:
    :prim_inet.recv0/3
    (postgrex) lib/postgrex/protocol.ex:2838: Postgrex.Protocol.msg_recv/4
    (postgrex) lib/postgrex/protocol.ex:1880: Postgrex.Protocol.recv_bind/3
    (postgrex) lib/postgrex/protocol.ex:1735: Postgrex.Protocol.bind_execute_close/4
    (db_connection) lib/db_connection/holder.ex:316: DBConnection.Holder.holder_apply/4
    (db_connection) lib/db_connection.ex:1272: DBConnection.run_execute/5
    (db_connection) lib/db_connection.ex:1359: DBConnection.run/6
    (db_connection) lib/db_connection.ex:613: DBConnection.execute/4
[error] Internal server error: %DBConnection.ConnectionError{message: "tcp recv: closed (the connection was closed by the pool, possibly due to a timeout or because the pool has been terminated)", reason: :error, severity: :error}
[info] Sent 500 in 15293ms
[error] #PID<■■■> running Pleroma.Web.Endpoint (connection #PID<■■■>, stream id 1) terminated
Server: nixeneko.info:80 (http)
Request: GET /api/v1/timelines/home?limit=80
** (exit) an exception was raised:
    ** (DBConnection.ConnectionError) tcp recv: closed (the connection was closed by the pool, possibly due to a timeout or because the pool has been terminated)
        (ecto_sql) lib/ecto/adapters/sql.ex:593: Ecto.Adapters.SQL.raise_sql_call_error/1
        (ecto_sql) lib/ecto/adapters/sql.ex:526: Ecto.Adapters.SQL.execute/5
        (ecto) lib/ecto/repo/queryable.ex:192: Ecto.Repo.Queryable.execute/4
        (ecto) lib/ecto/repo/queryable.ex:17: Ecto.Repo.Queryable.all/3
        (pleroma) lib/pleroma/pagination.ex:40: Pleroma.Pagination.fetch_paginated/4
        (pleroma) lib/pleroma/web/activity_pub/activity_pub.ex:1172: Pleroma.Web.ActivityPub.ActivityPub.fetch_activities/3
        (pleroma) lib/pleroma/web/mastodon_api/controllers/timeline_controller.ex:59: Pleroma.Web.MastodonAPI.TimelineController.home/2
        (pleroma) lib/pleroma/web/mastodon_api/controllers/timeline_controller.ex:5: Pleroma.Web.MastodonAPI.TimelineController.action/2

ここから、PostgreSQLで時間がかかっていることがわかる。

対策

検索してたら次の投稿を見つけた。
pleroma.gidikroon.eu

I think I remember that once after a migration I needed to do an ANALYZE to stop the timeouts from happening.

そのため、データベースのVACUUM ANALYZEを実行してみた。

VACUUM ANALYZEの実行

cd /opt/pleroma
sudo service pleroma stop
sudo -Hu pleroma MIX_ENV=prod mix pleroma.database vacuum analyze
sudo service pleroma start

参考: Database maintenance tasks - Pleroma Documentation

vacuum analyzeの直前にpg_dumpでバックアップをしている。pleromaはデータベース名、pleroma_database_backup.pgdumpは出力ファイル

sudo -Hu postgres pg_dump -d pleroma --format=custom -f pleroma_database_backup.pgdump

結果

すると、ホームタイムラインが復活した。
副作用として、うまく動かなくなっていたパブリックタイムラインとハッシュタグタイムラインが動くようになった。

データベースを移行した時とか、定期的にVACUUM ANALYZEを実行するといいようだ。