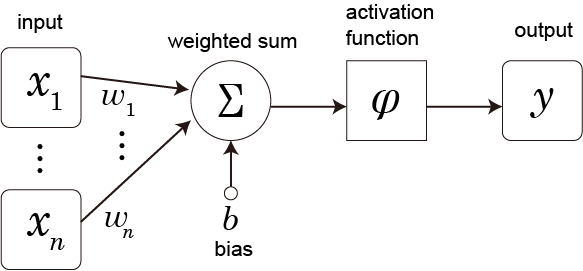
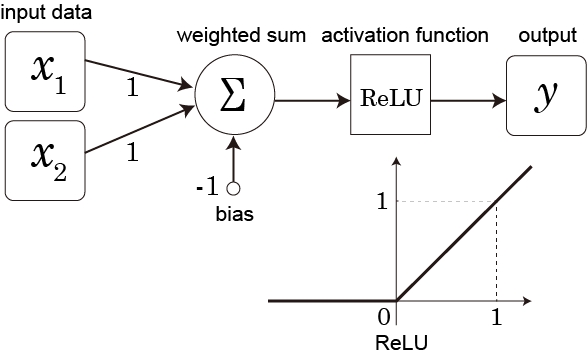
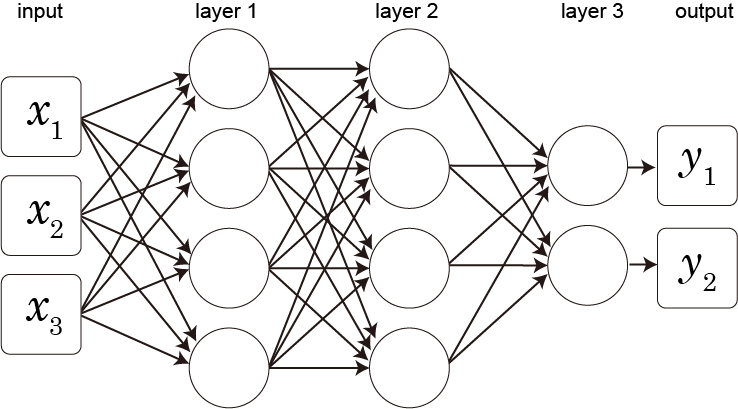
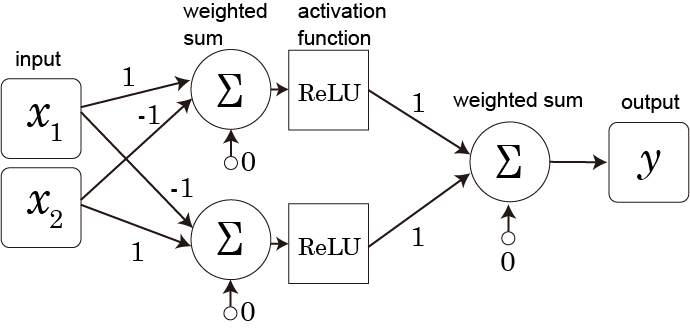
TrueType命令で遊ぶシリーズ。
- 初めてのTrueType命令: Windowsでは見えないフォントをつくる - にせねこメモ
- フォントサイズに合わせて回転するフォントを作る(1) - にせねこメモ
- PPEM・ポイントサイズを表示するフォント - にせねこメモ
- TrueType命令で三角関数(sin, cos)を計算する - にせねこメモ
- フォントサイズに合わせて回転するフォントを作る(2) - にせねこメモ
- TrueType命令で擬似乱数: 線形合同法 - にせねこメモ
- TrueType命令でビット演算 - にせねこメモ
擬似乱数を使って何か
前に擬似乱数を生成する関数を作ったので、それを使って何かやってみようというのが今回の目的である。
アウトラインをぶれさせてみたら、ランダムさが効果的に使えるのではないかと思うので、それをやってみる。
完成品

M+フォント(mplus-1p-regular.ttf)のアウトラインをガタガタにしている。フォントサイズによって文字の形が変わっているところに注目してほしい。
イラレとかで大きさを変えていくのを見ても面白い。
Adobe Illustrator CS6でこんな感じ。 pic.twitter.com/FqEdumiHSz
— にせねこ (@nixeneko) 2017年6月6日
実装
やっていることは単純で、各制御点の座標を読み出し、それに対して乱数生成関数によって生成した乱数を(適当にスケールして)足し合わせ、その座標に制御点を動かす。これをX, Y軸、および全ての制御点に対して行う。
さて、実際に実装してみる。
初期化
各種値の初期化は'prep'で行う。
まず、擬似乱数関数に与える初期seedを適当に初期化する。できるだけ乱雑になってほしかったのでMPPEM命令でPPEMを取得してそれを初期seedとした。これにより、フォントサイズによって乱数列が異なり、最終的に得られるアウトラインもフォントサイズ依存になる。
このseedをStorage Area 0番地に保存する。
次に、乱数のスケールに使用するscale factor を準備する。
XまたはY軸方向に移動する距離の最大値(つまり、スケール後の乱数の絶対値の最大)をCVTテーブルの0番に書いておく。ここでは30 (FUnits)とした。
これをRCVTで読みだすとpixel単位になるので、それをとする。
乱数の最大値は0x7FFFFFFFであるので、とする。
このとき、の場合に、
を計算する際にオーバーフローしてしまうため、それを防ぐために
という処理を入れている。
読みだした乱数をで割ることで、乱数(の絶対値)が0~pの範囲に含まれる様になる。
最後にscale factor をStorage Areaの1番地に保存している。
#seed初期化 PUSHB_1 0 MPPEM # 初期seed (>0) WS # StorageArea[0] = PPEM #スケール係数の初期化 PUSHW_7 #0xFF|256.0|0xFF|256.0|0xFF|256.0|0x7F| 255 # 0xFF 16384 # 256.0 255 # 0xFF 16384 # 256.0 255 # 0xFF 16384 # 256.0 127 # 0x7F MUL #0xFF|256.0|0xFF|256.0|0xFF|0x7F00| ADD #0xFF|256.0|0xFF|256.0|0x7FFF| MUL #0xFF|256.0|0xFF|0x7FFF00| ADD #0xFF|256.0|0x7FFFFF| MUL #0xFF|0x7FFFFF00| ADD #0x7FFFFFFF| #2147483647 = 0x7FFFFFFF PUSHB_1 0 RCVT #0x7FFFFFFF|CVT[0]| DUP #0x7FFFFFFF|CVT[0]|CVT[0]| PUSHB_1 #0x7FFFFFFF|CVT[0]|CVT[0]|1.0| 64 LT #0x7FFFFFFF|CVT[0]|CVT[0]<1.0| IF #0x7FFFFFFF|CVT[0]| #if CVT[0]<1.0: POP #0x7FFFFFFF| PUSHB_1 #0x7FFFFFFF|1.0| 64 EIF DIV #0x7FFFFFFF/CVT[0]| PUSHB_1 #0x7FFFFFFF/CVT[0]|1| 1 SWAP #1|0x7FFFFFFF/CVT[0]| WS #StorageArea[1] = 0x7FFFFFFF/CVT[0]
Storage Areaへの割り付け
| 番号 | value |
|---|---|
| 0 | seed (PPEMで初期化) |
| 1 | scale factor |
関数群
関数1: スケールした乱数の取得
関数0を呼び出して乱数を取得し、'prep'でStorage Areaの1番地に保存したscale factor で割ることでスケールする。
この際、取得した乱数を1ビット左シフトし、取得した乱数の上から2ビット目を符号ビットとして扱うことで、負の数も得られる様にしている。
最終的に得られる乱数は、最大動き幅pについて-p~pの範囲となるはず。
/* Function 1: returns scaled random value */ PUSHB_1 1 FDEF /* ..| *//* ← initial stack */ PUSHB_1 0 CALL /* ..|rand| */ DUP ADD /* ..|rand<<1| */ /* to make it signed */ PUSHB_1 1 RS /* ..|rand<<1|s| */ /*s = StorageArea[1], scaling factor */ DIV /* ..|(rand<<1)/s| */ ENDF
関数2: 指定された制御点をランダムな大きさだけ動かす
指定された制御点番号kに対応する制御点のX座標、Y座標を取得し、それに対して関数1で取得したスケール済み乱数を足しあわせ、計算された座標にSCFSで移動している。
/* Function 2: moves the control point k */ /* initial stack ..| k | k: 編集する制御点番号 */ /* final stack ..| */ PUSHB_1 2 FDEF /* ..|k| */ DUP /* ..|k|k| */ DUP /* ..|k|k|k| */ DUP /* ..|k|k|k|k| */ SVTCA[x-axis] /* X座標に設定 */ GC[cur] /* ..|k|k|k|x_k| */ PUSHB_1 1 CALL /* ..|k|k|k|x_k|rand| */ /* get scaled random value*/ ADD /* ..|k|k|k|x_k+rand| */ SCFS /* ..|k|k| */ /* 制御点kのX座標を x_k + rand に */ SVTCA[y-axis] /* Y座標に設定 */ GC[cur] /* ..|k|y_k| */ PUSHB_1 1 CALL /* ..|k|y_k|rand| */ ADD /* ..|k|y_k+rand| */ SCFS /* ..| */ /* 制御点kのY座標を y_k + rand に */ ENDF
関数3: カウントアップしつつ関数2を呼び出す
LOOPCALLで呼び出される用の関数。スタックトップの番号(カウンター)を引数として関数2を呼び出し、最後にカウンターを1増やす。
/* function 3: call func2 with value n and increment n */ /* initial stack: ..|n| */ /* final stack: ..|n+1| */ PUSHB_1 3 FDEF /* ..|n| */ /* repeat n times */ DUP /* ..|n|n| */ PUSHB_1 2 CALL /* ..|n| */ /* moves the point n */ PUSHB_1 /* ..|n|1| */ 1 ADD /* ..|n+1| */ ENDF
関数4: LOOPCALLで関数3を指定回数実行する
グリフから呼び出され、指定回数(=制御点の個数回)関数3を実行する。関数3では呼び出す度にスタックトップの値(カウンター)を1ずつ増やしていくので、すべての制御点に対して操作が行われることになる。
/* function 4: call func3 n times */ /* initial stack: ..|n| n: number of repetition */ /* final stack: ..| */ PUSHB_1 4 FDEF /* ..|n| */ /* n: num of points in the glyph */ PUSHB_1 /* ..|n|0| */ /* initialize the counter by 0 */ 0 SWAP /* ..|0|n| */ PUSHB_1 /* ..|0|n|3| */ 3 LOOPCALL /* ..| */ /* call function 3, n times */ ENDF
グリフ
関数4を、グリフから次のように呼び出す。
例えば、グリフに含まれる制御点の個数が10個であれば、
PUSHB_2 10 4 CALL
となる。
すべてのグリフへの適用
'cvt ', 'fpgm', 'prep'を設定して書き出したフォントAmovepointsrandom.ttfをttxを使ってXMLファイル(.ttx)にダンプする。
ttx Amovepointsrandom.ttf
その後、次のPythonプログラムを実行し、Amovepointsrandom.ttxのすべてのグリフに対して関数を呼び出すTrueType命令を適用した結果(Amovepointsrandom-out.ttx)を得る。
やっていることは、グリフ毎に制御点の個数を調べ、その値を組み込んだ関数呼び出しの命令を付加するという感じ。
#!/usr/bin/env python3 # conding: utf-8 import xml.etree.ElementTree as ET INFILE = "Amovepointsrandom.ttx" OUTFILE = "Amovepointsrandom-out.ttx" xmltree = ET.parse(INFILE) xmlroot = xmltree.getroot() for glyph in xmlroot.find('glyf').findall('TTGlyph'): cnt = 0 for contour in glyph.findall('contour'): cnt += len(contour.findall('pt')) if cnt > 0: prog =""" PUSHB[ ] /* 2 values pushed */ {} 4 CALL[ ] /* CallFunction */ """.format(cnt) glyph.find('instructions').find('assembly').text = prog with open(OUTFILE, 'w') as w: w.write('<?xml version="1.0" encoding="UTF-8"?>\n') xmlstr = ET.tostring(xmlroot, method='xml', encoding="unicode") #xmltree.write(OUTFILE) w.write(xmlstr)
最後に得られた.ttxファイルをttxで.ttfに変換する。
ttx Amovepointsrandom-out.ttx
これによって生成されるAmovepointsrandom-out.ttfが完成品である。
コード
'fpgm'
PUSHB_1 0 FDEF PUSHB_1 0 RS DUP PUSHW_2 30000 14488 ADD DUP ROLL SWAP PUSHW_1 4096 MUL DIV ROLL ROLL PUSHB_1 3 CINDEX PUSHW_1 4096 MUL MUL SUB PUSHW_3 4096 30000 18271 ADD MUL MUL SWAP PUSHW_2 3399 4096 MUL MUL SUB DUP PUSHB_1 0 GT IF ELSE PUSHW_7 255 16384 255 16384 255 16384 127 MUL ADD MUL ADD MUL ADD ADD EIF DUP PUSHB_1 0 SWAP WS ENDF PUSHB_1 1 FDEF PUSHB_1 0 CALL DUP ADD PUSHB_1 1 RS DIV ENDF PUSHB_1 2 FDEF DUP DUP DUP SVTCA[x-axis] GC[cur] PUSHB_1 1 CALL ADD SCFS SVTCA[y-axis] GC[cur] PUSHB_1 1 CALL ADD SCFS ENDF PUSHB_1 3 FDEF DUP PUSHB_1 2 CALL PUSHB_1 1 ADD ENDF PUSHB_1 4 FDEF PUSHB_1 0 SWAP PUSHB_1 3 LOOPCALL ENDF
'prep'
PUSHB_1 0 MPPEM WS PUSHW_7 255 16384 255 16384 255 16384 127 MUL ADD MUL ADD MUL ADD PUSHB_1 0 RCVT DUP PUSHB_1 64 LT IF POP PUSHB_1 64 EIF DIV PUSHB_1 1 SWAP WS