2017-02-13

OpenTypeフォントで万年カレンダーをつくる

OpenType フォント

はじめに

カレンダーの一つの月の日付の並びには、各曜日始まりの7種×日数の種類(28, 29, 30, 31日)の4種で合計28種ある。祝日などを考えなければ28種を使いまわすことで任意の年月に対応できる。

そんな発想で作られた、使いまわしできるカレンダーを万年カレンダーという(日数の違いにまで対応してるとは限らないが)。
という訳で、せっかくなのでこの万年カレンダーをOpenTypeフォントで実装してみる。

2016-01とか2016/01とか書くと2016年1月のカレンダーが表示されるようにしたい。

完成品

f:id:nixeneko:20170211002007p:plain

Webフォントによる表示

2017/02

Javascriptでカウントアップさせてみる:

2000/01

たのしい！

ダウンロード

Acalendar.ttf (72.9 KB)

ソースコード

GitHubに挙げたのでそちらを参照。
github.com

Acalendar.ttf: フォントデータ
Acalendar.sfd: Fontforgeファイル (GSUB, GPOSの設定なし)
calendar.fea: GSUB, GPOSの定義

仕様・制限

OpenType機能の'liga', 'mkmk'を有効にして表示する。
“2017/02”, “12345/6” などといった、

(年)/(月)

の形に対応している。

年は正数にしか対応していない*1。
6桁以上の年数はOpenTypeの'mkmk'フィーチャを有効にできる環境でないとうまく年が表示できない。
年が15桁以上だと月の表示と被る可能性がある。
月は2桁または1桁に対応している。
スラッシュはハイフンでもよい。

正規表現で表すと

\d+[-/]\d{1,2}

となる。

方針

togetter.com
ここで色々検討されているが、カレンダーが28種類のなかからどれを使うかは、

その年の元日の曜日は何か
その年は閏年かどうか
何月か

によって決まる。
元日の曜日は400年ごとに同じ並びが繰り返され、次のような計算式で計算できるっぽい。(なお、日曜のoffset=3は間違い)

正整数Yについて、Y年1月1日の曜日wは、 y' = Y - 1 mod 400 w = y' + ⌊y' / 4⌋ - ⌊y' / 100⌋ + offset mod 7 で求められるっぽい。ただしoffset=2だと土曜が0, offset=3だと日曜が0となる。
— にせねこ (@nixeneko) 2017年1月2日

閏年かどうかは、西暦の年の数字が

400で割り切れるときは閏年
400で割り切れない、かつ、100で割り切れるときは閏年ではない
400で割り切れない、かつ、100で割り切れない、かつ、4で割り切れるときは閏年
それ以外は(4で割り切れないとき)は閏年ではない

という風に判定でき、

4で割り切れる
100で割り切れる
400で割り切れる

かどうかの3つを組み合わせて判定できる。

OpenTypeのGSUBによる置換を使って剰余等の計算を真面目に行ってもいいのだろうが、非常に面倒臭そうだし、状態の数が結構な数になってしまいそうなので、今回は西暦の年を400で割った余りについて、400通りの置換を定義することで行う。3桁未満にも対応できるように実際には置換の数はもっと増える(というか、499個)。

実装

グリフの用意

実装してみる。
アウトラインとしてM+ Fontsの mplus-1p-medium.ttf をベースにした。

まずは始まる曜日の違い(7種)と月の日数の違い(4種)で28種類のカレンダーを用意する。
最初にグリフの用意。
日曜始まりでカレンダーを用意した。
始まる曜日と日数で、グリフ名を

cal_mon_28

など、

cal_(曜日)_(日数)

とした。

GSUBの実装

詳しくは、GitHubに上げた calendar.fea を参照されたい。

最初に年について400の剰余を計算する。
これは要するに、百の位以上の桁について4の剰余を計算すればよい。

4の剰余を表すための状態の数だけ状態に対応する数字のグリフを作成する。

数字	0	1	2	3	4	5	6	7	8	9
0 mod 4	0₀	1₀	2₀	3₀	4₀	5₀	6₀	7₀	8₀	9₀
1 mod 4	0₁	1₁	2₁	3₁	4₁	5₁	6₁	7₁	8₁	9₁
2 mod 4	0₂	1₂	2₂	3₂	4₂	5₂	6₂	7₂	8₂	9₂
3 mod 4	0₃	1₃	2₃	3₃	4₃	5₃	6₃	7₃	8₃	9₃

実際には zero_0mod4, one_0mod4, …, nine_0mod4, …, zero_3mod4, …, nine_3mod4 などという名前のグリフを用意した。

数字の並びについて、まず前に数字が続かないもの、つまり数字の最初の桁について置換をおこなう。3桁の数字の最初の文字について次のように置換をおこなう。

元の数字	0	1	2	3	4	5	6	7	8	9
置換先	0₀	1₁	2₂	3₃	4₀	5₁	6₂	7₃	8₀	9₁

これは lookup check_first_fig_mod4 で行っている。

次に、4の剰余の状態を持った数字の次に来る3つの数字のうちの1番目の数字について置換を行う。
つまり、
mod4の数字 普通の数字 普通の数字普通の数字
という並びの時に太字にした“普通の数字”を対応するmod4の数字に置換する。

元の数字	0	1	2	3	4	5	6	7	8	9
前が剰余0か2の時の置換先	0₀	1₁	2₂	3₃	4₀	5₁	6₂	7₃	8₀	9₁
前が剰余1か3の時の置換先	0₂	1₃	2₀	3₁	4₂	5₃	6₀	7₁	8₂	9₃

これは lookup check_mod4 で行った。
これで年の400の剰余が求まった。

さて、次に、年の始まりの曜日と閏年かどうかの14状態を判定する。これは、その14状態に対応するスラッシュ“/”のグリフを用意し、年と月の間のスラッシュ“/”(あるいはハイフンでもいい)に対し置換を行うこととする。これはスラッシュの前3桁の数字について400通り(数字が2桁、1桁しかない場合を加えて499通り)の置換をずらずら列挙することになる。うっ頭が…。
これは lookup check_firstday_and_leapyear で実装した。気合、といった感じ。
状態をもつスラッシュのグリフ名は

slash_mon_leap
slash_tue_comm

などとした。(mon, tue, wed, thu, fri, sat, sun)×(leap, comm)

置換後、スラッシュが14の状態をもっている。閏年はl, 閏年でない年はnで示した。
スラッシュの14状態(一番左の列)に対して、後続する数字(一番上の行)によって次の表のようにカレンダーを表示する。表記したのはカレンダーに含まれる日数と開始曜日である。

	01	02	03	04	05	06	07	08	09	10	11	12
日, n	31日	28水	31水	30土	31月	30木	31土	31火	30金	31日	30水	31金
月, n	31月	28木	31木	30日	31火	30金	31日	31水	30土	31月	30木	31土
火, n	31火	28金	31金	30月	31水	30土	31月	31木	30日	31火	30金	31日
水, n	31水	28土	31土	30火	31木	30日	31火	31金	30月	31水	30土	31月
木, n	31木	28日	31日	30水	31金	30月	31水	31土	30火	31木	30日	31火
金, n	31金	28月	31月	30木	31土	30火	31木	31日	30水	31金	30月	31水
土, n	31土	28火	31火	30金	31日	30水	31金	31月	30木	31土	30火	31木
日, l	31日	29水	31木	30日	31火	30金	31日	31水	30土	31月	30木	31土
月, l	31月	29木	31金	30月	31水	30土	31月	31木	30日	31火	30金	31日
火, l	31火	29金	31土	30火	31木	30日	31火	31金	30月	31水	30土	31月
水, l	31水	29土	31日	30水	31金	30月	31水	31土	30火	31木	30日	31火
木, l	31木	29日	31月	30木	31土	30火	31木	31日	30水	31金	30月	31水
金, l	31金	29月	31火	30金	31日	30水	31金	31月	30木	31土	30火	31木
土, l	31土	29火	31水	30土	31月	30木	31土	31火	30金	31日	30水	31金

14 × 12 = 168通り。一桁の数字にも対応するために126通りの置換を追加し計294通りになった。
これは lookup replace_calendar で行った。

さて、カレンダーを表示するのもいいけどせっかくなので何年何月ってのも表示させたい。
月については、事前に月を示す(JAN, FEB, などと表示される)グリフを用意しておき、グリフ幅0で、カレンダーのグリフの次にきたときに丁度いい位置に月の表示がくるように位置調整しておく。
これを、カレンダーのグリフに後続する2桁または1桁の数字に対して置換をおこなうことで、月の表示を可能にしている。
これは lookup replace_month で実装した。

最後に年の表示。数字をspacingなグリフにしてしまうと、並べるのは簡単だが、左側に空白ができてしまう。
という訳で、年の数字専用の幅0のグリフを用意しておき、GSUBで数字をそれらのグリフに置換し、その後GPOSのMarkToMark positioning (タグでいうと'mkmk')を使って位置調整することで年の数字を並べようと考えた。

さて、フォントが一応できたので動作を見てみる。

Adobe InDesign

「文字」パネルプルダウンメニューから「欧文合字」をオンにすると……
f:id:nixeneko:20170208224745p:plain
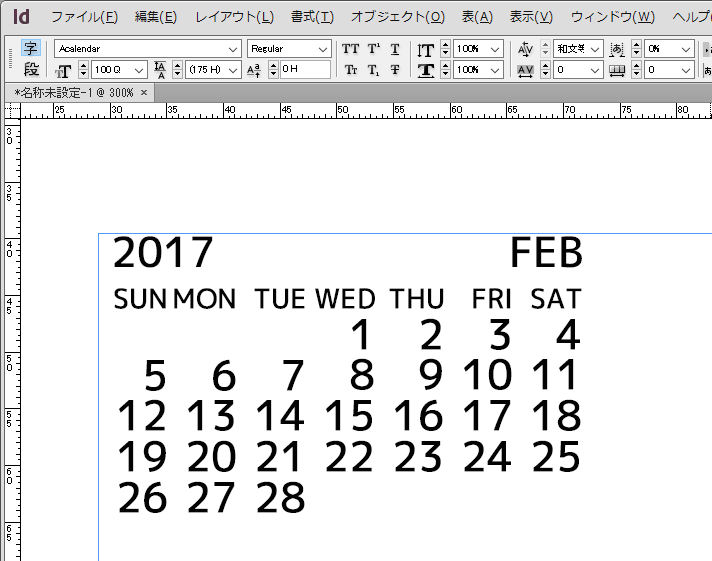
やったー！

Adobe Illustrator

イラレではどうかな？OpenTypeパネルから欧文合字を有効にして……
f:id:nixeneko:20170208225148p:plain
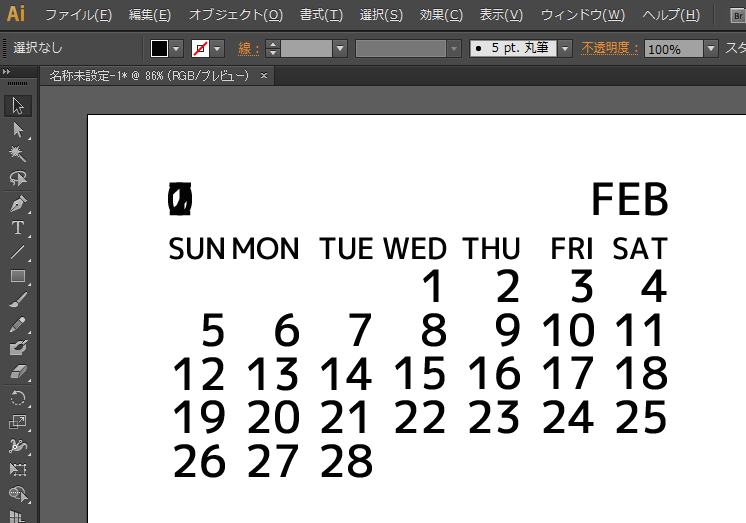
あれー？
'mkmk'が効いてない。
もし'mark'は効くであれば、'mkmk'じゃなくても'mark'とGSUBによる置換で代用することはできるのだけれど。

今回は、GSUBだけである程度まで動くようにしておく。事前に位置をずらした数字を用意しておいて、GSUBで順番に置換する。5桁あれば十分だろう。それより大きい桁数は'mkmk'を有効にできる環境で使うようにしてもらう。
これによって年を表す数字のグリフが5倍に増える。
このあたりは lookup replace_year_10000, lookup replace_year によってGSUB置換を実装、さらに lookup STACK_YEAR を使って6桁以上の年の数字が右に並ぶようにした。

結果

Adobe Illustrator

f:id:nixeneko:20170209182717p:plain
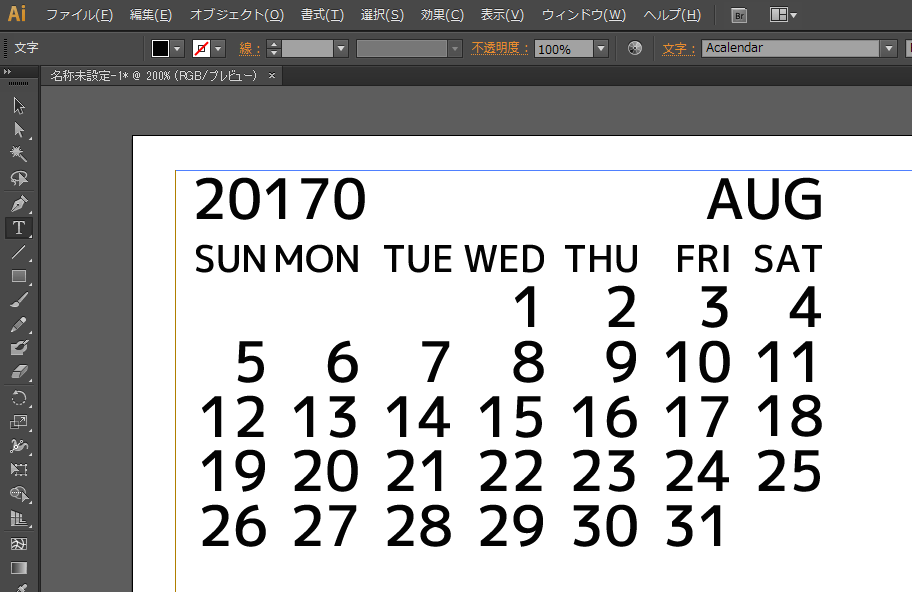
やったー！
もちろん年が6桁以上になるのは文字が重なってうまく表示できないのだけど(10万年後もグレゴリオ暦が使われてるのか、閏年の計算も同じなのか謎だけど)。

Adobe InDesign

f:id:nixeneko:20170209183216p:plain
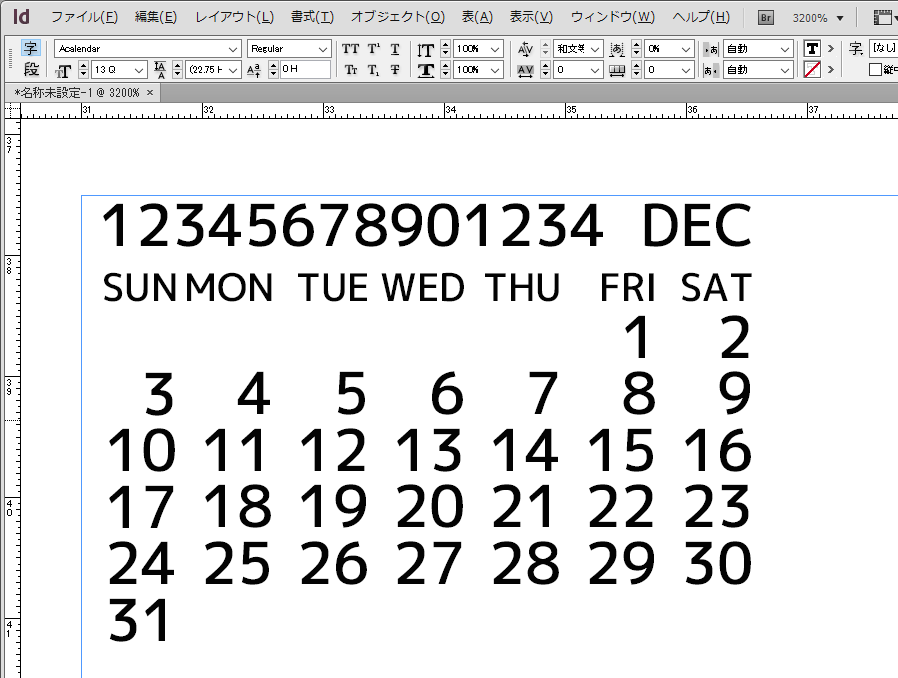
もちろんInDesignでは6桁以上も'mkmk'でうまく並ぶ。 $10^{13}$ 年後も地球が存在してるのか知らんけど。ちなみに太陽の寿命が $10^{10}$ 年位らしい。

*1:とはいえ、紀元前にグレゴリオ暦を適用してどうするのって気もする……。

2017-02-09

WindowsでChainerのセットアップ

Python Windows

ZOTAC GeForce GTX 1060を買った。ので、最近話題のchainerをセットアップしたメモ。

環境

OS: Windows 10 (64 bit)
Python: Python3 (Anaconda Windows 64-bit)

今までつけてたQuadro K600も刺してある。

GTX 1060のセットアップ

取り付け
CDのドライバをインストール

最新版Nvidiaドライバのインストール
- Driver version 378.49 (当時)
- http://www.nvidia.co.jp/Download/index.aspx?lang=jp

Visual Studioのインストール

Visual Studio 2015は既に入っていたので省略。

CUDAのインストール

CUDA Toolkit 8.0のインストール

https://developer.nvidia.com/cuda-downloads

ウィザードに従ってインストールする。

もしかしてここで間違ってドライバを入れてしまったかもしれない。NVidia GeForce Experienceとかいうソフトが最新のドライバをサジェストしてくるので何度かインストールしたり再起動を繰り返したりなどした。

cuDNNのインストール

https://developer.nvidia.com/cudnn

ダウンロードするためには登録が必要。

ダウンロードしてきたzipファイルの中身のcudaディレクトリ以下を

C:\Program Files\NVIDIA GPU Computing Toolkit\CUDA\v8.0

の下に突っ込む。

Anaconda Pythonを最新に

Anacondaを最新版に更新。
Anaconda Promptを開いて

conda update conda
conda update --all

Chainerのインストール

環境変数の

PATHに C:\Program Files (x86)\Microsoft Visual Studio 14.0\VC\bin
INCLUDEに C:\Program Files (x86)\Windows Kits\10\Include\10.0.10240.0\ucrt

を追加。

Windows 10にCUDA 8.0 RCとChainerをインストール – Secret Laboratory

(追記: 下はv1の時の手順、あるいはv2でGPUを利用しない場合)
Anaconda Promptから

pip install chainer --no-cache-dir

と実行する。

2017-06-10 追記

Chainer 2.0から、CuPyとChainerが別パッケージに分離された。そのため、pipでchainerだけでなくcupyも一緒にインストールしないとGPUが使えない。

v1系から更新する場合には、Anaconda Promptから

pip uninstall chainer
pip install cupy chainer --no-cache-dir

とする。

(追記終)

テスト

chainer/example/mnist/ のMNISTのサンプルをダウンロードしてきて実行。

CPU (Core i7-3770)が20 iters/sec、GTX 1060が130～170 iters/sec、Quadro K600が50 iters/sec位だった。案外Quadro K600がGTX 1060の3分の1位の速度出てるっぽいし、CUDAコア数が10倍になったからといって速度が10倍にはならない。ボトルネックはどこだろう。

参考

Windows 10にCUDA 8.0 RCとChainerをインストール – Secret Laboratory

2017-02-07

フォントサイズに合わせて回転するフォントを作る(2)

TrueType フォント

TrueType命令で遊ぶシリーズ。

はじめに

さて、前回作った回転するフォントでは回転の処理があまり賢くないので、それを改善するのがこの記事でやりたいことである。
そのために、三角関数のsin, cosの値を計算する関数を作成した。この関数を利用して回転行列の要素の値を計算し、それによって回転するという風にする。

成果物

f:id:nixeneko:20170205130752p:plain

イラレではあまり見たことのない動きをする。正直気持ち悪い。笑 pic.twitter.com/3jU229mSND
— にせねこ (@nixeneko) 2017年2月5日

きもい実にきもい。

ダウンロード

Arotate.ttf (1.74 MB)

変更点

回転行列の値のStorage Areaへの格納

三角関数(sin, cos)を計算する関数を関数4としてもってきた。
他は、基本的に前回の回転するフォントそのままであるが、'prep'での回転行列の要素の値を格納する際に、PPEMの値を取得し、その角度に対する三角関数の計算を呼び出し、その結果を格納している。

'prep'

/* prep */
MPPEM         /* |ppem(int)| */
PUSHW_1 4096  /* |ppem(int)|64.0| */
MUL           /* |ppem(F26Dot6)| */
PUSHB_1 4     /* |ppem(F26Dot6)|4| */
CALL          /* |64*sin|64*cos| */
PUSHB_2 2 3   /* |64*sin|64*cos|2|3| */
ROLL          /* |64*sin|2|3|64*cos| */
WS            /* |64*sin|2| */ /* StorageArea[3] = 64*cos */
SWAP          /* |2|64*sin| */
WS            /* |          */ /* StorageArea[2] = 64*sin */

MPPEMで取得したppemの値に適当な係数を掛け算してやると、回転の度合いを調整できる。マイナスをかければ逆回転になる。

回転

関数2で回転した座標を計算する際に、前回はLOOPCALLを用いていたが、ここは今回は1回だけ回転させればいいので、CALLに変更している。
ついでに関数2で引数として余計なスタック要素が積まれてたのを削除している。

'fpgm'

PUSHB_1
 0
FDEF          /* ..| n-1 |             *//* ← initial stack */
PUSHB_1       /* ..| n-1 | 2 |         */ 
 2
ADD           /* ..| n+1 |             *//* n+1: phantom point n+1 に対応 */
SVTCA[x-axis]                            /* 座標の測定をx軸方向にする */
GC[orig]      /* ..| x_(n+1) |         *//* phantom point n+1の(X)座標取得 */
PUSHB_1       /* ..| x_(n+1) | 2.0 |   *//* Uint 128 == F24Dot6 2.0 */
 128
DIV           /* ..| x_(n+1) / 2 |     */
PUSHB_1       /* ..| x_(n+1) / 2 | 0 | */
 0
SWAP          /* ..| 0 | x_(n+1) / 2 | */
WS            /* ..|                   *//* StorageArea[0] = x_(n+1) / 2 */
PUSHB_1       /* ..| 1 |               */
 1
RCVT          /* ..| CVT[1] |          *//* read control value table */
PUSHB_1       /* ..| CVT[1] | 1 |      */     /* CVT[1]は回転中心y_cに対応 */
 1
SWAP          /* ..| 1 | CVT[1] |      */
WS            /* ..|                   *//* StorageArea[1] = CVT[1] */
ENDF

/* Function 1: Calculates rotated coordinates with pre-defined angle T */
/* initial stack ..| y | x |             x' = x*cosT - y*sinT          */
/* final stack   ..| y'| x'|      while  y' = x*sinT + y*cosT          */
PUSHB_1
 1
FDEF     /* ..|y|x|                                 */
DUP      /* ..|y|x|x|                               */
ROLL     /* ..|x|x|y|                               */
DUP      /* ..|x|x|y|y|                             */
ROLL     /* ..|x|y|y|x|                             */
PUSHB_1  /* ..|x|y|y|x|3|                           */
 3
RS       /* ..|x|y|y|x|64*cosT|                     */ /* SA[3] = 64*cosT */
MUL      /* ..|x|y|y|64*x*cosT|                     */
SWAP     /* ..|x|y|64*x*cosT|y|                     */
PUSHB_1  /* ..|x|y|64*x*cosT|y|2|                   */
 2
RS       /* ..|x|y|64*x*cosT|y|64*sinT|             */ /* SA[2] = 64*sinT */
MUL      /* ..|x|y|64*x*cosT|64*y*sinT|             */
SUB      /* ..|x|y|64*(x*cosT - y*sinT)|            */
PUSHW_1  /* ..|x|y|64*(x*cosT - y*sinT)|64.0|       */
 4096
DIV      /* ..|x|y|x*cosT - y*sinT|                 */
ROLL     /* ..|y|x*cosT - y*sinT|x|                 */
ROLL     /* ..|x*cosT - y*sinT|x|y|                 */
PUSHB_1  /* ..|x*cosT - y*sinT|x|y|3|               */
 3
RS       /* ..|x*cosT - y*sinT|x|y|64*cosT|         */ /* SA[3] = 64*cosT */
MUL      /* ..|x*cosT - y*sinT|x|64*y*cosT|         */
SWAP     /* ..|x*cosT - y*sinT|64*y*cosT|x|         */
PUSHB_1  /* ..|x*cosT - y*sinT|64*y*cosT|x|2|       */
 2
RS       /* ..|x*cosT - y*sinT|64*y*cosT|x|64*sinT| */ /* SA[2] = 64*sinT */
MUL      /* ..|x*cosT - y*sinT|64*y*cosT|64*x*sinT| */
ADD      /* ..|x*cosT - y*sinT|64*(x*sinT + y*cosT)| */
PUSHW_1  /* ..|x*cosT - y*sinT|64*(x*sinT + y*cosT)|64.0| */
 4096
DIV      /* ..|x*cosT - y*sinT|x*sinT + y*cosT|     */
SWAP     /* ..|x*sinT + y*cosT|x*cosT - y*sinT|     */ 
ENDF                        /* ↑関数呼び出し時とx, yの順番を合わせている */

/* Function 2: moves a control point k to the rotated coordinates         */
/* initial stack ..| k |       k: 編集する制御点番号                           */
/* final stack   ..|                                                      */
PUSHB_1
 2
FDEF     /* ..|k| */
DUP      /* ..|k|k| */
DUP      /* ..|k|k|k| */
SVTCA[x-axis]                                  /* X座標に設定 */
GC[cur]  /* ..|k|k|x_k| */
SWAP     /* ..|k|x_k|k| */
SVTCA[y-axis]                                  /* Y座標に設定 */
GC[cur]  /* ..|k|x_k|y_k| */
PUSHB_1  /* ..|k|x_k|y_k|1| */
 1
RS       /* ..|k|x_k|y_k|y_c|           */ /* y_c = SA[1]: 回転中心Y座標 */
SUB      /* ..|k|x_k|y_k-y_c|           */
SWAP     /* ..|k|y_k-y_c|x_k|           */
PUSHB_1  /* ..|k|y_k-y_c|x_k|0|         */
 0
RS       /* ..|k|y_k-y_c|x_k|x_c|       */ /* x_c = SA[0]: 回転中心X座標 */
SUB      /* ..|k|y_k-y_c|x_k-x_c|       */
PUSHB_1  /* ..|k|y_k-y_c|x_k-x_c|1|*/
 1
CALL     /* ..|k|y_k-y_c|x_k-x_c|       */ /* call function 1 */
             /* y_k' = y_k-y_c, x_k' = x_k-x_c are changed to y_k'', x_k'' */
PUSHB_1  /* ..|k|y_k''|x_k''|0|         */ 
 0
RS       /* ..|k|y_k''|x_k''|x_c|       */ /* x_c = SA[0]: 回転中心X座標 */
ADD      /* ..|k|y_k''|x_k''+x_c|       */
SWAP     /* ..|k|x_k''+x_c|y_k''|       */
PUSHB_1  /* ..|k|x_k''+x_c|y_k''|1|     */
 1
RS       /* ..|k|x_k''+x_c|y_k''|y_c|   */ /* y_c = SA[1]: 回転中心Y座標 */
ADD      /* ..|k|x_k''+x_c|y_k''+y_c|   */
SVTCA[y-axis]                                 /* Y座標に設定 */
PUSHB_1  /* ..|k|x_k''+x_c|y_k''+y_c|3| */ 
 3
CINDEX   /* ..|k|x_k''+x_c|y_k''+y_c|k| * stack先頭から3番目をトップにコピー*/
SWAP     /* ..|k|x_k''+x_c|k|y_k''+y_c| */
SCFS     /* ..|k|x_k''+x_c|            *//* 制御点kのY座標を y_k''+y_c に */
SVTCA[x-axis]                                 /* X座標に設定 */
SCFS     /* ..|                        *//* 制御点kのX座標を x_k''+x_c に */
ENDF


PUSHB_1
 3
FDEF      /* ..|n-1|           */
DUP       /* ..|n-1|n-1|       */
PUSHB_1   /* ..|n-1|n-1|0|     */
 0
CALL      /* ..|n-1|           */ /* call function 0 */
DUP       /* ..|n-1|i|         */ /* i = n-1 とおく */ 
                                  /* jump_to_here */
DUP       /* ..|n-1|i|i|       */
PUSHB_1   /* ..|n-1|i|i|0|     */
 0
GTEQ      /* ..|n-1|i|i<0|     */
IF        /* ..|n-1|i|         */ /* if i<0 then */
  DUP     /* ..|n-1|i|i|       */
  PUSHB_1 /* ..|n-1|i|i|2|     */
   2
  CALL    /* ..|n-1|i|         */ /* call function 2 */ 
  PUSHB_1 /* ..|n-1|i|1|       */ 
   1
  SUB     /* ..|n-1|i-1|       */
  PUSHW_1 /* ..|n-1|i-1|-15|   */
    -15
  JMPR    /* ..|n-1|i-1|       */ /* goto jump_to_here */
EIF                               /* end if */
POP       /* ..|n-1|           */
POP       /* ..|               */
ENDF

/* function 4 は省略、前回の記事参照 */

ソース

'fpgm'

PUSHB_1
 0
FDEF
PUSHB_1
 2
ADD
SVTCA[x-axis]
GC[orig]
PUSHB_1
 128
DIV
PUSHB_1
 0
SWAP
WS
PUSHB_1
 1
RCVT
PUSHB_1
 1
SWAP
WS
ENDF
PUSHB_1
 1
FDEF
DUP
ROLL
DUP
ROLL
PUSHB_1
 3
RS
MUL
SWAP
PUSHB_1
 2
RS
MUL
SUB
PUSHW_1
 4096
DIV
ROLL
ROLL
PUSHB_1
 3
RS
MUL
SWAP
PUSHB_1
 2
RS
MUL
ADD
PUSHW_1
 4096
DIV
SWAP
ENDF
PUSHB_1
 2
FDEF
DUP
DUP
SVTCA[x-axis]
GC[cur]
SWAP
SVTCA[y-axis]
GC[cur]
PUSHB_1
 1
RS
SUB
SWAP
PUSHB_1
 0
RS
SUB
PUSHB_1
 1
CALL
PUSHB_1
 0
RS
ADD
SWAP
PUSHB_1
 1
RS
ADD
SVTCA[y-axis]
PUSHB_1
 3
CINDEX
SWAP
SCFS
SVTCA[x-axis]
SCFS
ENDF
PUSHB_1
 3
FDEF
DUP
PUSHB_1
 0
CALL
DUP
DUP
PUSHB_1
 0
GTEQ
IF
DUP
PUSHB_1
 2
CALL
PUSHB_1
 1
SUB
PUSHW_1
 -15
JMPR
EIF
POP
POP
ENDF
PUSHB_1
 4
FDEF
DUP
PUSHW_1
 23040
GTEQ
IF
PUSHW_1
 23040
SUB
PUSHW_1
 -13
JMPR
EIF
DUP
PUSHB_1
 0
LT
IF
PUSHW_1
 23040
ADD
PUSHW_1
 -12
JMPR
EIF
PUSHB_2
 64
 64
ROLL
DUP
PUSHW_1
 11520
GT
IF
PUSHW_1
 23040
SWAP
SUB
ROLL
NEG
ROLL
ROLL
EIF
DUP
PUSHW_1
 5760
GT
IF
PUSHW_1
 11520
SWAP
SUB
SWAP
NEG
SWAP
EIF
DUP
PUSHB_1
 0
EQ
IF
POP
PUSHW_2
 0
 4096
ELSE
DUP
PUSHW_1
 5760
EQ
IF
POP
PUSHW_2
 4096
 0
ELSE
NPUSHW
 10
 57
 114
 229
 458
 916
 1833
 3666
 7331
 14648
 29184
PUSHW_4
 8340
 3
 16384
 4096
MUL
MUL
ADD
PUSHW_4
 10506
 6
 16384
 4096
MUL
MUL
ADD
PUSHW_4
 4096
 11
 16384
 4096
MUL
MUL
ADD
PUSHB_1
 14
MINDEX
PUSHW_1
 4096
MUL
PUSHW_2
 4096
 4096
PUSHB_1
 0
PUSHB_1
 64
PUSHB_1
 6
MINDEX
ROLL
PUSHB_1
 1
ADD
ROLL
PUSHB_1
 128
MUL
ROLL
PUSHB_1
 3
CINDEX
PUSHB_1
 12
LTEQ
IF
PUSHB_1
 5
MINDEX
PUSHB_1
 5
MINDEX
DUP
PUSHB_1
 5
CINDEX
DIV
PUSHB_1
 3
CINDEX
PUSHB_1
 6
CINDEX
DIV
ROLL
SWAP
PUSHB_1
 5
CINDEX
PUSHB_1
 9
CINDEX
LT
IF
ADD
ROLL
ROLL
SUB
SWAP
PUSHB_1
 5
MINDEX
PUSHB_1
 5
MINDEX
PUSHB_1
 5
MINDEX
PUSHB_1
 7
MINDEX
ADD
ELSE
SUB
ROLL
ROLL
ADD
SWAP
PUSHB_1
 5
MINDEX
PUSHB_1
 5
MINDEX
PUSHB_1
 5
MINDEX
PUSHB_1
 7
MINDEX
SUB
EIF
PUSHW_1
 -85
JMPR
EIF
POP
POP
POP
PUSHW_1
 6745
DUP
ROLL
PUSHW_1
 4096
MUL
SWAP
DIV
ROLL
PUSHW_1
 4096
MUL
ROLL
DIV
ROLL
POP
EIF
EIF
ROLL
MUL
ROLL
ROLL
MUL
SWAP
ENDF

'prep'

MPPEM
PUSHW_1
 4096
MUL
PUSHB_1
 4
CALL
PUSHB_2
 2
 3
ROLL
WS
SWAP
WS

'cvt '

index	val
0	0
1	379

グリフ固有のプログラム

PUSHB_2
 11
 3
CALL

11の部分にはそのグリフの最大の制御点番号が入る。

2017-02-05

TrueType命令で三角関数(sin, cos)を計算する

TrueType

TrueType Instructionで遊ぶシリーズ。
初めてのTrueType命令: Windowsでは見えないフォントをつくる - にせねこメモ
 フォントサイズに合わせて回転するフォントを作る(1) - にせねこメモ
 PPEM・ポイントサイズを表示するフォント - にせねこメモ

TrueType Instructionを使って回転を計算したい。そうなると当然三角関数が使いたくなる。一方でTrueType Instruction Setには三角関数を計算する命令は入っていない。そのため自前で計算する必要がある。

方針

さて、自前で計算するにはどうすればいいだろうか？方法はいくつかある。
一つはMaclaurin展開(あるいはTaylor展開)によって計算するもの(たぶんこっちのが実装は楽)。
一つはCORDICというアルゴリズム(計算方法について調べてるときに教えてもらった)。
どちらも四則演算のみによって計算できる。

今回はCORDICというアルゴリズムを使ってみる。これは非負整数 $i \in \mathbb{N}_{0}$ について $\tan\theta_i = \frac{1}{2^i}$ となるような $\theta_i=\mathrm{atan}\left(\frac{1}{2^i}\right)$ の値を事前にテーブルとして持っておいて、その値に四則演算をしていくことで、最終的な関数を得るというものらしい*1。テーブルとして持つ $i$ の上限は必要とする精度によって決める。詳しくは次のサイトを参考にされたい。

関数電卓コラム 10/02/24 関数電卓のしくみ(CORDICアルゴルズム)

F26Dot6の精度

さて、TrueType命令で使える小数フォーマットはF26Dot6(以降Q6とも書く)、すなわち整数部が26ビットで小数部が6ビットである固定小数点数である。
Q6の値は整数と同様の扱いであるが、 $2^6 = 64$ だけ下駄がはかされていると考えるとよい。すなわち、Q6を整数として解釈した数値を64で割ると実際の数値が求まる。
例えばQ6フォーマットで表される数値を整数で表現すると、Q6の1.0は整数の64、Q6の2.0は整数の128、Q6の0.75は整数の48、などとなる。

TrueType命令において、足し算(ADD[ ])・引き算(SUB[ ])は整数に対して定義されている。これは小数点の位置を変化させないため固定小数点数に対してもそのまま使える。
一方で掛け算(MUL[ ])や割り算(DIV[ ])はF26Dot6に対して定義されていて、計算結果もF26Dot6である。これは、実際には次のような計算が行われるとのことである。

A * B: (n₁ * n₂) / 64
A / B: (n₁ * 64) / n₂

n₁, n₂は整数として扱われ、基本的に整数同士の掛け算あるいは割り算と同様であるが、固定小数点数なので右端(LSB)から6ビットが小数部であることを考慮して、最終的な計算結果がF26Dot6となるように、適当なところで64で割ったり64を掛けたりして桁を調整している。64で割るのは6ビット分算術右シフトすることと同等で、64掛けるのは6bit分左シフトするのと同等であるが、TrueType命令にビットシフト演算はない。

ところで、A*Bの場合は計算結果を64で割っていて、A/Bの場合はAに64を掛けている。仕様に記載があるかもしれないし、または実装に依るのかもしれないが、32bit整数型で計算していた場合、A*Bの先頭6bitは桁あふれによって、またA/BにおけるAの先頭6ビットのデータについてもデータが失われた状態になりそうな気がする。そう考えると、乗除算で実質に使えるのは26ビット程度(20Dot6、つまり-524288.～524287.程度)になるかもしれない。大きな数値を扱う必要がある場合には問題になる可能性があるかもしれない。

それにしても、フォントの制御点を表すためとはいえ、小数部が6bitというのはかなり心もとない気がする。 $2^6 = 0.015625$ であるから、10進数で0.01の細かさは表現できないことになる。さすがに $\sin$ や $\cos$ を計算するのにこれだと心許ない気がするので、さらに6bit分下駄をはかせて20Dot12 (Q12)相当として計算していくことにする。乗除算を計算する際には上で示したようにF26Dot6用で計算されるため、出力される数値の小数点の位置を適宜調整する必要がでてくることに気を付けないといけない。

CORDICアルゴリズムの実装

定数のストア

まず使用する定数類をStorage Areaに保存して、プログラム内から読み出すことを考えてみる。
Storage Areaへの割り付けは次のようにする。定数には6ビット分(=64)だけ下駄をはかせている。

index	value	備考
0	0x2D000	$64\theta_0 = \mathrm{atan}\left(\frac{1}{2^0}\right)$
1	0x1A90A	$64\theta_1 = \mathrm{atan}\left(\frac{1}{2^1}\right)$
2	0xE094	$64\theta_2 = \mathrm{atan}\left(\frac{1}{2^2}\right)$
3	0x7200	$64\theta_3 = \mathrm{atan}\left(\frac{1}{2^3}\right)$
4	0x3938	$64\theta_4 = \mathrm{atan}\left(\frac{1}{2^4}\right)$
5	0x1CA3	$64\theta_5 = \mathrm{atan}\left(\frac{1}{2^5}\right)$
6	0x0E52	$64\theta_6 = \mathrm{atan}\left(\frac{1}{2^6}\right)$
7	0x0729	$64\theta_7 = \mathrm{atan}\left(\frac{1}{2^7}\right)$
8	0x0394	$64\theta_8 = \mathrm{atan}\left(\frac{1}{2^8}\right)$
9	0x01CA	$64\theta_9 = \mathrm{atan}\left(\frac{1}{2^9}\right)$
10	0x00E5	$64\theta_{10} = \mathrm{atan}\left(\frac{1}{2^{10}}\right)$
11	0x0072	$64\theta_{11} = \mathrm{atan}\left(\frac{1}{2^{11}}\right)$
12	0x0039	$64\theta_{12} = \mathrm{atan}\left(\frac{1}{2^{12}}\right)$
13	0x1A59	$r_{12}$

定数なので'prep'でstoreしてしまおう。

ここで、PUSHWでは1ワード(16 bit)が符号拡張されるため、すなわち1ワードの最上位ビットが符号ビットとなるため、0x8000以上の数値はそのままPUSHWを使ってスタックに積むことはできない。例えば、

(上14ビット)*2^14 + (下14ビット)

みたいに値を分割してPUSHして後で合成してやらないといけない。

'prep'

PUSHB_1 /* store dest */
0
PUSHW_4
0x1000  /* 0x2D000 % 2^14 */
0x000B  /* 0x2D000 / 2^14 */
0x4000  /* 0x100.0 */
0x1000  /* 0x40.0 */
MUL
MUL
ADD
WS

PUSHB_1 /* store dest */
1
PUSHW_4
0x290A  /* 0x1A90A % 2^14 */
0x0006  /* 0x1A90A / 2^14 */
0x4000  /* 0x100.0 */
0x1000  /* 0x40.0 */
MUL
MUL
ADD
WS


PUSHB_1 /* store dest */
2
PUSHW_4
0x2094  /* 0xE094 % 2^14 */
0x0003  /* 0xE094 / 2^14 */
0x4000  /* 0x100.0 */
0x1000  /* 0x40.0 */
MUL
MUL
ADD
WS

PUSHB_1 /* store dest */
3
PUSHW_1
0x7200
WS

PUSHB_1 /* store dest */
4
PUSHW_1
0x3938
WS

PUSHB_1 /* store dest */
5
PUSHW_1
0x1CA3
WS

PUSHB_1 /* store dest */
6
PUSHW_1
0x0E52
WS

PUSHB_1 /* store dest */
7
PUSHW_1
0x0729
WS

PUSHB_1 /* store dest */
8
PUSHW_1
0x0394
WS

PUSHB_1 /* store dest */
9
PUSHW_1
0x01CA
WS

PUSHB_1 /* store dest */
10
PUSHW_1
0x00E5
WS

PUSHB_1 /* store dest */
11
PUSHW_1
0x0072
WS

PUSHB_1 /* store dest */
12
PUSHW_1
0x0039
WS

PUSHB_1 /* store dest */
13
PUSHW_1
0x1A59
WS

計算の実装

さて、CORDICアルゴリズムで実際に計算をする部分の実装に入る。
入力は角度 ${\theta[\mbox{°}]}$ (F26Dot6)、出力は $64\cdot\sin\theta, 64\cdot\cos\theta$ (F26Dot6)とする。
入力となる角度 ${\theta[\mbox{°}]}$ は $0 \le \theta \le 90$ の範囲にあるものとする。

Pythonで書くとこんな感じになる。

import math

# constants 定数格納部分
theta = [math.atan(1.0 / (2**x)) * 180 / math.pi for x in range(13)]
rsq = [2.0]
for i in range(1,13):
    rsq.append(rsq[-1] + rsq[-1]/(2.0**(2*i)))
r = list(map(math.sqrt, rsq))

# calculate sin, cos 計算部分
deg = 30 #input angle 入力の角度 [0,90]
d = theta[0] # current temporary angle
x = 1.0
y = 1.0
for i in range(1,13):
    lastx = x
    lasty = y
    if d > deg:
        d = d - theta[i]
        x = lastx + lasty/(2**i)
        y = lasty - lastx/(2**i)
    else:
        d = d + theta[i]
        x = lastx - lasty/(2**i)
        y = lasty + lastx/(2**i)

mycos = x/r[12] #cos計算結果
mysin = y/r[12] #sin計算結果

#print("mycos:", mycos, ", mysin:", mysin)
#print("  cos:", math.cos(deg/180*math.pi), ",   sin:", math.sin(deg/180*math.pi))

定数格納はしたので、計算部分を実装する。

最初に入力 $\theta$ を与えて、それに対応する $\sin\theta, \cos\theta$ を計算するような次のプログラムをつくった。

PUSHW_1 1920 /* theta=30.0 */ /* input angle */



             /* ...|theta| */
PUSHW_1 4096 /* ...|theta|64.0| */
MUL          /* ...|64t| */ /* 64t = 64*theta, 更に6ビット下駄を履かす */

PUSHW_2      /* ...|64t|64*1.0|64*1.0| */ 
 4096 
 4096 
PUSHB_1 0    /* ...|64t|64*1.0|64*1.0|0| */
DUP          /* ...|64t|64*1.0|64*1.0|0|0| */
RS           /* ...|64t|64*1.0|64*1.0|0|64t0| *//*t0=theta_0=StorageArea[0]*/
PUSHB_1 64   /* ...|64t|64*1.0|64*1.0|0|64t0|1.0| */
SWAP         /* ...|64t|64*1.0|64*1.0|0|1.0|64t0| */
             /* ...|64t|64x=64*1.0|64y=64*1.0|i=0|2.0^i=1.0|ti=64t0| */
             /* i: counter,   2.0^i: 冪関数やビットシフト演算の代替*/
             /* ti: current angle */
/* L0: */
/* i = i+1, 2.0^i = 2.0^(i+1) に更新 */  
ROLL         /* ...|64t|64x|64y|2.0^i|64ti|i| */ 
PUSHB_1 1    /* ...|64t|64x|64y|2.0^i|64ti|i|1| */
ADD          /* ...|64t|64x|64y|2.0^i|64ti|i+1| */
ROLL         /* ...|64t|64x|64y|64ti|i+1|2.0^i| */
PUSHB_1 128  /* ...|64t|64x|64y|64ti|i+1|2.0^i|2.0| */
MUL          /* ...|64t|64x|64y|64ti|i+1|2.0^(i+1)| */
ROLL         /* ...|64t|64x|64y|i+1|2.0^(i+1)|64ti| */

/* if i <= 12  */
PUSHB_1 3
CINDEX       /* ...|64t|64x|64y|i|2.0^i|64ti|i| */
PUSHB_1 12   /* ...|64t|64x|64y|i|2.0^i|64ti|i|12| */
LTEQ         /* ...|64t|64x|64y|i|2.0^i|64ti|i<=12| */
IF           /* ...|64t|64x|64y|i|2.0^i|64ti| */ /* if (i <= 12) */
  
  PUSHB_1 5
  MINDEX     /* ...|64t|64y|i|2.0^i|64ti|64x| */
  PUSHB_1 5
  MINDEX     /* ...|64t|i|2.0^i|64ti|64x|64y| */
  DUP        /* ...|64t|i|2.0^i|64ti|64x|64y|64y| */
  PUSHB_1 5
  CINDEX     /* ...|64t|i|2.0^i|64ti|64x|64y|64y|2.0^i| */
  DIV        /* ...|64t|i|2.0^i|64ti|64x|64y|64y/2.0^i| */
  PUSHB_1 3
  CINDEX     /* ...|64t|i|2.0^i|64ti|64x|64y|64y/2.0^i|64x| */
  PUSHB_1 6
  CINDEX     /* ...|64t|i|2.0^i|64ti|64x|64y|64y/2.0^i|64x|2.0^i| */
  DIV        /* ...|64t|i|2.0^i|64ti|64x|64y|64y/2.0^i|64x/2.0^i| */

  ROLL       /* ...|64t|i|2.0^i|64ti|64x|64y/2.0^i|64x/2.0^i|64y| */
  SWAP       /* ...|64t|i|2.0^i|64ti|64x|64y/2.0^i|64y|64x/2.0^i| */

  /* if (ti<t) { */
  PUSHB_1 5
  CINDEX     /* ...|64t|i|2.0^i|64ti|64x|64y/2.0^i|64y|64x/2.0^i|64ti| */
  PUSHB_1 9
  CINDEX     /* ...|64t|i|2.0^i|64ti|64x|64y/2.0^i|64y|64x/2.0^i|64ti|64t| */
  LT         /* ...|64t|i|2.0^i|64ti|64x|64y/2.0^i|64y|64x/2.0^i|64ti<64t| */
  IF         /* ...|64t|i|2.0^i|64ti|64x|64y/2.0^i|64y|64x/2.0^i| */ 
    /* if ti<t */

    /* x -= y/(2^i) , y+= x/(2^i)*/
    ADD      /* ...|64t|i|2.0^i|64ti|64x|64y/2.0^i|64y+64x/2.0^i| */
    ROLL     /* ...|64t|i|2.0^i|64ti|64y/2.0^i|64y+64x/2.0^i|64x| */
    ROLL     /* ...|64t|i|2.0^i|64ti|64y+64x/2.0^i|64x|64y/2.0^i| */
    SUB      /* ...|64t|i|2.0^i|64ti|64y+64x/2.0^i|64x-64y/2.0^i| */
    SWAP     /* ...|64t|i|2.0^i|64ti|64x-64y/2.0^i|64y+64x/2.0^i| */
    PUSHB_1 5
    MINDEX   /* ...|64t|2.0^i|64ti|64x-64y/2.0^i|64y+64x/2.0^i|i| */
    PUSHB_1 5
    MINDEX   /* ...|64t|64ti|64x-64y/2.0^i|64y+64x/2.0^i|i|2.0^i| */
    PUSHB_1 5
    MINDEX   /* ...|64t|64x-64y/2.0^i|64y+64x/2.0^i|i|2.0^i|64ti| */
    
    /* ti = ti+thetai */
    PUSHB_1 3
    CINDEX   /* ...|64t|64x-64y/2.0^i|64y+64x/2.0^i|i|2.0^i|64ti|i| */
    RS       /* ...|64t|64x-64y/2.0^i|64y+64x/2.0^i|i|2.0^i|64ti|theta_i| */
    ADD      /* ...|64t|64x-64y/2.0^i|64y+64x/2.0^i|i|2.0^i|64ti+theta_i| */ 

  ELSE /* if it>= t */

    /* x += y/(2^i) , y-= x/(2^i)*/
    SUB      /* ...|64t|i|2.0^i|64ti|64x|64y/2.0^i|64y-64x/2.0^i| */
    ROLL     /* ...|64t|i|2.0^i|64ti|64y/2.0^i|64y-64x/2.0^i|64x| */
    ROLL     /* ...|64t|i|2.0^i|64ti|64y-64x/2.0^i|64x|64y/2.0^i| */
    ADD      /* ...|64t|i|2.0^i|64ti|64y-64x/2.0^i|64x+64y/2.0^i| */
    SWAP     /* ...|64t|i|2.0^i|64ti|64x+64y/2.0^i|64y-64x/2.0^i| */
    PUSHB_1 5
    MINDEX   /* ...|64t|2.0^i|64ti|64x+64y/2.0^i|64y-64x/2.0^i|i| */
    PUSHB_1 5
    MINDEX   /* ...|64t|64ti|64x+64y/2.0^i|64y-64x/2.0^i|i|2.0^i| */
    PUSHB_1 5
    MINDEX   /* ...|64t|64x+64y/2.0^i|64y-64x/2.0^i|i|2.0^i|64ti| */

    /* ti = ti-theta_i */
    PUSHB_1 3
    CINDEX   /* ...|64t|64x+64y/2.0^i|64y-64x/2.0^i|i|2.0^i|64ti|i| */
    RS       /* ...|64t|64x+64y/2.0^i|64y-64x/2.0^i|i|2.0^i|64ti|theta_i| */
    SUB      /* ...|64t|64x+64y/2.0^i|64y-64x/2.0^i|i|2.0^i|64ti-theta_i| */ 

  EIF
  PUSHW_1 -87
  JMPR       /*goto L0*/
EIF
             /* ...|64t|64x|64y|i|2.0^i|64ti| */
POP          /* ...|64t|64x|64y|i|2.0^i| */
POP          /* ...|64t|64x|64y|i| */
POP          /* ...|64t|64x|64y| */
PUSHB_1 13   /* ...|64t|64x|64y|13| */
RS           /* ...|64t|64x|64y|64r_12| */ /* 64r_12=StorageArea[13] */
DUP          /* ...|64t|64x|64y|64r_12|64r_12| */
ROLL         /* ...|64t|64x|64r_12|64r_12|64y| */
PUSHW_1 4096 /* ...|64t|64x|64r_12|64r_12|64y|64.0| */
MUL          /* ...|64t|64x|64r_12|64r_12|64*64y| */
SWAP         /* ...|64t|64x|64r_12|64*64y|64r_12| */
DIV          /* ...|64t|64x|64r_12|64sin| */ /* 64sin = 64*y/r_12 */
ROLL         /* ...|64t|64r_12|64sin|64x| */
PUSHW_1 4096 /* ...|64t|64r_12|64sin|64x|64.0| */
MUL          /* ...|64t|64r_12|64sin|64*64x| */
ROLL         /* ...|64t|64sin|64*64x|64r_12| */
DIV          /* ...|64t|64sin|64cos| */ /* 64cos = 64*x/r_12 */
ROLL         /* ...|64sin|64cos|64t| */
POP          /* ...|64sin|64cos| */

やっぱStorage Area使わない方がいいよね

Storage Area使うと、他の関数や命令で使う値を潰してしまうかもしれないので、あまりよろしくない。という訳で、Storage Area使わない版もつくった。

theta_iの定数には、順番に、かつ1回しかアクセスしないため、スタックの下の方に定数を先に使う方が上になるように積んでおいて(theta_12, theta_11, ..., theta_1, theta_0)、MINDEXで若い順にスタックトップに取り出して使うようにした。
MINDEXはスタックトップから数えるので、ループでも、毎回同じ番号を指定することで定数に順番にアクセスできる。

PUSHW_1 1920 /* 30 deg */ /*入力として与える角度*/


/* stack: ...|theta| */
/* PUSH constants */
NPUSHW 10
 0x0039
 0x0072
 0x00E5
 0x01CA
 0x0394
 0x0729
 0x0E52
 0x1CA3
 0x3938
 0x7200
PUSHW_4
 0x2094  /* 0xE094 % 2^14 */
 0x0003  /* 0xE094 / 2^14 */
 0x4000  /* 0x100.0 */
 0x1000  /* 0x40.0 */
MUL
MUL
ADD
PUSHW_4
 0x290A  /* 0x1A90A % 2^14 */
 0x0006  /* 0x1A90A / 2^14 */
 0x4000  /* 0x100.0 */
 0x1000  /* 0x40.0 */
MUL
MUL
ADD
PUSHW_4
 0x1000  /* 0x2D000 % 2^14 */
 0x000B  /* 0x2D000 / 2^14 */
 0x4000  /* 0x100.0 */
 0x1000  /* 0x40.0 */
MUL
MUL
ADD
             /* ...|theta|theta_12|theta_11|...|theta_0| */


PUSHB_1 14
MINDEX       /* ...|64theta_12|...|64theta_0|theta| */
PUSHW_1 4096 /* ...|64theta_12|...|64theta_0|theta|64.0| */
MUL          /* ...|64theta_12|...|64theta_0|64t| */ /* 64t=64*theta */
             /* ...|64theta_i|64t| */

PUSHW_2      /* ...|64theta_0|64t|64*1.0|64*1.0| */
 4096
 4096 
PUSHB_1 0
PUSHB_1 64   /* ...|64theta_0|64t|64*1.0|64*1.0|i=0|1.0| */
PUSHB_1 6  
MINDEX       /* ...|64theta_1|64t|64*1.0|64*1.0|i=0|1.0|64theta_0| */ 
   /* ...|64theta_i|64t|64x=64*1.0|64y=64*1.0|i=0|2.0^i=1.0|64ti=64theta_0| */

/*L0:*/ 
/* i = i+1, 2.0^i = 2.0^(i+1) に更新 */  
             /* ...|64t|64x|64y|i|2.0^i|64ti| */ 
ROLL         /* ...|64t|64x|64y|2.0^i|64ti|i| */ /* i++ */
PUSHB_1 1    /* ...|64t|64x|64y|2.0^i|64ti|i|1| */
ADD          /* ...|64t|64x|64y|2.0^i|64ti|i+1| */
ROLL         /* ...|64t|64x|64y|64ti|i+1|2.0^i| */
PUSHB_1 128  /* ...|64t|64x|64y|64ti|i+1|2.0^i|2.0| */
MUL          /* ...|64t|64x|64y|64ti|i+1|2.0^(i+1)| */
ROLL         /* ...|64t|64x|64y|i+1|2.0^(i+1)|64ti| */

/* if i <= 12  */
PUSHB_1 3
CINDEX       /* ...|64t|64x|64y|i|2.0^i|64ti|i| */
PUSHB_1 12   /* ...|64t|64x|64y|i|2.0^i|64ti|i|12| */
LTEQ         /* ...|64t|64x|64y|i|2.0^i|64ti|i<=12| */
IF           /* ...|64t|64x|64y|i|2.0^i|64ti| */ /* if (i <= 12) */

  PUSHB_1 5
  MINDEX     /* ...|64t|64y|i|2.0^i|64ti|64x| */
  PUSHB_1 5
  MINDEX     /* ...|64t|i|2.0^i|64ti|64x|64y| */
  DUP        /* ...|64t|i|2.0^i|64ti|64x|64y|64y| */
  PUSHB_1 5
  CINDEX     /* ...|64t|i|2.0^i|64ti|64x|64y|64y|2.0^i| */
  DIV        /* ...|64t|i|2.0^i|64ti|64x|64y|64y/2.0^i| */
  PUSHB_1 3
  CINDEX     /* ...|64t|i|2.0^i|64ti|64x|64y|64y/2.0^i|64x| */
  PUSHB_1 6
  CINDEX     /* ...|64t|i|2.0^i|64ti|64x|64y|64y/2.0^i|64x|2.0^i| */
  DIV        /* ...|64t|i|2.0^i|64ti|64x|64y|64y/2.0^i|64x/2.0^i| */

  ROLL       /* ...|64t|i|2.0^i|64ti|64x|64y/2.0^i|64x/2.0^i|64y| */
  SWAP       /* ...|64t|i|2.0^i|64ti|64x|64y/2.0^i|64y|64x/2.0^i| */

  /* if (ti<t) { */
  PUSHB_1 5
  CINDEX     /* ...|64t|i|2.0^i|64ti|64x|64y/2.0^i|64y|64x/2.0^i|64ti| */
  PUSHB_1 9
  CINDEX     /* ...|64t|i|2.0^i|64ti|64x|64y/2.0^i|64y|64x/2.0^i|64ti|64t| */
  LT         /* ...|64t|i|2.0^i|64ti|64x|64y/2.0^i|64y|64x/2.0^i|64ti<64t| */
  IF         /* ...|64t|i|2.0^i|64ti|64x|64y/2.0^i|64y|64x/2.0^i| */ 
    /* if ti<t */

    /* x -= y/(2^i) , y+= x/(2^i)*/
    ADD      /* ...|64t|i|2.0^i|64ti|64x|64y/2.0^i|64y+64x/2.0^i| */
    ROLL     /* ...|64t|i|2.0^i|64ti|64y/2.0^i|64y+64x/2.0^i|64x| */
    ROLL     /* ...|64t|i|2.0^i|64ti|64y+64x/2.0^i|64x|64y/2.0^i| */
    SUB      /* ...|64t|i|2.0^i|64ti|64y+64x/2.0^i|64x-64y/2.0^i| */
    SWAP     /* ...|64t|i|2.0^i|64ti|64x-64y/2.0^i|64y+64x/2.0^i| */
    PUSHB_1 5
    MINDEX   /* ...|64t|2.0^i|64ti|64x-64y/2.0^i|64y+64x/2.0^i|i| */
    PUSHB_1 5
    MINDEX   /* ...|64t|64ti|64x-64y/2.0^i|64y+64x/2.0^i|i|2.0^i| */
    PUSHB_1 5
    MINDEX   /* ...|64t|64x-64y/2.0^i|64y+64x/2.0^i|i|2.0^i|64ti| */

    /* ti = ti+theta_i */
    PUSHB_1 7
    MINDEX   /* ...|64t|64x-64y/2.0^i|64y+64x/2.0^i|i|2.0^i|64ti|theta_i| */
    ADD      /* ...|64t|64x-64y/2.0^i|64y+64x/2.0^i|i|2.0^i|64ti+theta_i| */ 

  ELSE /* if it>= t */

    /* x += y/(2^i) , y-= x/(2^i)*/
    SUB      /* ...|64t|i|2.0^i|64ti|64x|64y/2.0^i|64y-64x/2.0^i| */
    ROLL     /* ...|64t|i|2.0^i|64ti|64y/2.0^i|64y-64x/2.0^i|64x| */
    ROLL     /* ...|64t|i|2.0^i|64ti|64y-64x/2.0^i|64x|64y/2.0^i| */
    ADD      /* ...|64t|i|2.0^i|64ti|64y-64x/2.0^i|64x+64y/2.0^i| */
    SWAP     /* ...|64t|i|2.0^i|64ti|64x+64y/2.0^i|64y-64x/2.0^i| */
    PUSHB_1 5
    MINDEX   /* ...|64t|2.0^i|64ti|64x+64y/2.0^i|64y-64x/2.0^i|i| */
    PUSHB_1 5
    MINDEX   /* ...|64t|64ti|64x+64y/2.0^i|64y-64x/2.0^i|i|2.0^i| */
    PUSHB_1 5
    MINDEX   /* ...|64t|64x+64y/2.0^i|64y-64x/2.0^i|i|2.0^i|64ti| */

    /* ti = ti-theta_i */
    PUSHB_1 7
    MINDEX   /* ...|64t|64x+64y/2.0^i|64y-64x/2.0^i|i|2.0^i|64ti|theta_i| */
    SUB      /* ...|64t|64x+64y/2.0^i|64y-64x/2.0^i|i|2.0^i|64ti-theta_i| */ 

  EIF
  PUSHW_1 -85
  JMPR  /*goto L0*/
EIF
             /* ...|64t|64x|64y|i|2.0^i|64ti| */
POP          /* ...|64t|64x|64y|i|2.0^i| */
POP          /* ...|64t|64x|64y|i| */
POP          /* ...|64t|64x|64y| */
PUSHW_1      /* ...|64t|64x|64y|64r_12| */ /* 64*r12 */
 0x1A59 
DUP          /* ...|64t|64x|64y|64r_12|64r_12| */
ROLL         /* ...|64t|64x|64r_12|64r_12|64y| */
PUSHW_1 4096 /* 64.0 */
MUL          /* ...|64t|64x|64r_12|64r_12|64*64y| */
SWAP         /* ...|64t|64x|64r_12|64*64y|64r_12| */
DIV          /* ...|64t|64x|64r_12|64sin| */ /* 64sin = 64*y/r_12 */
ROLL         /* ...|64t|64r_12|64sin|64x| */
PUSHW_1 4096 /* 64.0 */
MUL          /* ...|64t|64r_12|64sin|64*64x| */
ROLL         /* ...|64t|64sin|64*64x|64r_12| */
DIV          /* ...|64t|64sin|64cos| */ /* 64cos = 64*x/r_12 */
ROLL         /* ...|64sin|64cos|64t| */
POP          /* ...|64sin|64cos| */

計算の定義域の拡大

さて、0～90度の範囲だけしか計算できないというのはよろしくないので、これ以外の範囲にも対応できるようにする。

最初に、 $\theta$ が $0\le \theta < 360$ の範囲に入るようにする。
これは、三角関数が $2\pi$ の周期関数であることから、自然数nについて
$\sin(\theta) = \sin(\theta-2n\pi)$
$\cos(\theta) = \cos(\theta-2n\pi)$
が成り立つことによる。つまり、 $\theta$ が

360以上 → 360未満になるまで360を引く
0未満 → 0以上になるまで360を足す

         /* stack: ...|theta(F26Dot6)| */

/* L1: */
DUP             /* ...|theta|theta| */ 
PUSHW_1 23040   /* ...|theta|theta|360.0| */
GTEQ            /* ...|theta|theta>=360.0| */
IF              /* ...|theta| */ /* if (theta >= 360.0) */
  PUSHW_1 23040 /* ...|theta|360.0| */
  SUB           /* ...|theta-360.0| */
  PUSHW_1 -13   /* ...|theta-360.0|-13| */
  JMPR          /* ...|theta-360.0| */ /* goto L1 */
EIF

/* L2: */
DUP             /* ...|theta|theta| */ 
PUSHB_1 0       /* ...|theta|theta|0.0| */
LT              /* ...|theta|theta<0.0| */
IF              /* ...|theta| */ /* if (theta < 0.0) */
  PUSHW_1 23040 /* ...|theta|360.0| */
  ADD           /* ...|theta+360.0| */
  PUSHW_1 -12   /* ...|theta+360.0|-12| */
  JMPR          /* ...|theta+360.0| */ /* goto L2 */
EIF

PUSHB_2 64 64 /* ...|theta|sign_sin=1.0|sign_cos=1.0| */
ROLL /* ...|sign_sin|sign_cos|theta| */

最後でsinとcosに対応する符号(1.0で初期化)をスタックに用意した。これは次で利用する。

次に、 $180 < \theta < 360$ の場合に対応する。
$\sin\theta = -\sin(2\pi-\theta)$
$\cos\theta = \cos(2\pi-\theta)$
となることより、 $180 < \theta < 360$ の場合は、

$\theta := 360 - \theta$
sinの符号を反転

DUP /* ...|sign_sin|sign_cos|theta|theta| */
PUSHW_1 11520 /* ...|sign_sin|sign_cos|theta|theta|180.0| */
GT  /* ...|sign_sin|sign_cos|theta|theta>180.0| */
IF  /* ...|sign_sin|sign_cos|theta| */ /* if (theta>180.0) */
  PUSHW_1 23040 /* ...|sign_sin|sign_cos|theta|360.0| */
  SWAP  /* ...|sign_sin|sign_cos|360.0|theta| */
  SUB   /* ...|sign_sin|sign_cos|360.0-theta| */
  ROLL  /* ...|sign_cos|360.0-theta|sign_sin| */
  NEG   /* ...|sign_cos|360.0-theta|-sign_sin| */
  ROLL  /* ...|360.0-theta|-sign_sin|sign_cos| */
  ROLL  /* ...|-sign_sin|sign_cos|360.0-theta| */
EIF

次に、 $90 < \theta \le 180$ のときに対応する。
$\sin\theta = \sin(\pi - \theta)$
$\cos\theta = -\cos(\pi - \theta)$
となることより、 $90 < \theta \le 180$ となるときは、

$\theta := 180 - \theta$
cosの符号を反転

DUP /* ...|sign_sin|sign_cos|theta|theta| */
PUSHW_1 5760 /* ...|sign_sin|sign_cos|theta|theta|90.0| */
GT  /* ...|sign_sin|sign_cos|theta|theta>90.0| */
IF  /* ...|sign_sin|sign_cos|theta| */ /* if (theta>90.0) */
  PUSHW_1 11520 /* ...|sign_sin|sign_cos|theta|180.0| */
  SWAP  /* ...|sign_sin|sign_cos|180.0|theta| */
  SUB   /* ...|sign_sin|sign_cos|180.0-theta| */
  SWAP  /* ...|sign_sin|180.0-theta|sign_cos| */
  NEG   /* ...|sign_sin|180.0-theta|-sign_cos| */
  SWAP  /* ...|sign_sin|-sign_cos|180.0-theta| */
EIF

0度と90度の時は場合分けして値を出すようにしてみた。まあそんなことしなくても結構な精度で計算してくれるのだけれど。
/* CORDIC algorithm comes here */ の部分は、実際には上で作ったようなCORDICアルゴリズムによる角度計算のプログラムを入れる。

DUP         /* ...|sign_sin|sign_cos|theta|theta| */
PUSHB_1 0   /* ...|sign_sin|sign_cos|theta|theta|0.0| */
EQ          /* ...|sign_sin|sign_cos|theta|theta==0.0| */
IF          /* ...|sign_sin|sign_cos|theta| */ /* if (theta == 0.0) */
  POP       /* ...|sign_sin|sign_cos| */
  PUSHW_2   /* ...|sign_sin|sign_cos|0.0|64.0| */ 
   0
   4096 
            /* ...|sign_sin|sign_cos|64sin0 = 0|64cos0 = 64*1.0| */
ELSE
  DUP       /* ...|sign_sin|sign_cos|theta|theta| */
  PUSHW_1   /* ...|sign_sin|sign_cos|theta|theta|90.0| */
   5760
  EQ        /* ...|sign_sin|sign_cos|theta|theta==90.0| */
  IF        /* ...|sign_sin|sign_cos|theta| */ /* if (theta==90.0) */
    POP     /* ...|sign_sin|sign_cos| */
    PUSHW_2 /* ...|sign_sin|sign_cos|64.0|0.0| */
     4096 
     0
            /* ...|sign_sin|sign_cos|sin90 = 64.0|cos90 = 0.0| */
  ELSE /* theta != 0.0 and theta != 90.0 */
            /* ...|sign_sin|sign_cos|theta| */

    /* CORDIC algorithm comes here */

            /* ...|sign_sin|sign_cos|64sin|64cos| */
  EIF
EIF         /* ...|sign_sin|sign_cos|64sin|64cos| */

ROLL        /* ...|sign_sin|64sin|64cos|sign_cos| */
MUL         /* ...|sign_sin|64sin|sign_cos*64cos| */
ROLL        /* ...|64sin|sign_cos*64cos|sign_sin| */
ROLL        /* ...|sign_cos*64cos|sign_sin|64sin| */
MUL         /* ...|sign_cos*64cos|sign_sin*64sin| */
SWAP        /* ...|sign_sin*64sin|sign_cos*64cos| */

関数化

さて、これらの計算を関数としてまとめる。関数0とした。

initial stack: ...|angle (deg) (F26Dot6)|
  final stack: ...|64*sin|64*cos|

PUSHB_1
 0
FDEF
DUP
PUSHW_1
 23040
GTEQ
IF
PUSHW_1
 23040
SUB
PUSHW_1
 -13
JMPR
EIF
DUP
PUSHB_1
 0
LT
IF
PUSHW_1
 23040
ADD
PUSHW_1
 -12
JMPR
EIF
PUSHB_2
 64
 64
ROLL
DUP
PUSHW_1
 11520
GT
IF
PUSHW_1
 23040
SWAP
SUB
ROLL
NEG
ROLL
ROLL
EIF
DUP
PUSHW_1
 5760
GT
IF
PUSHW_1
 11520
SWAP
SUB
SWAP
NEG
SWAP
EIF
DUP
PUSHB_1
 0
EQ
IF
POP
PUSHW_2
 0
 4096
ELSE
DUP
PUSHW_1
 5760
EQ
IF
POP
PUSHW_2
 4096
 0
ELSE
NPUSHW
 10
 57
 114
 229
 458
 916
 1833
 3666
 7331
 14648
 29184
PUSHW_4
 8340
 3
 16384
 4096
MUL
MUL
ADD
PUSHW_4
 10506
 6
 16384
 4096
MUL
MUL
ADD
PUSHW_4
 4096
 11
 16384
 4096
MUL
MUL
ADD
PUSHB_1
 14
MINDEX
PUSHW_1
 4096
MUL
PUSHW_2
 4096
 4096
PUSHB_1
 0
PUSHB_1
 64
PUSHB_1
 6
MINDEX
ROLL
PUSHB_1
 1
ADD
ROLL
PUSHB_1
 128
MUL
ROLL
PUSHB_1
 3
CINDEX
PUSHB_1
 12
LTEQ
IF
PUSHB_1
 5
MINDEX
PUSHB_1
 5
MINDEX
DUP
PUSHB_1
 5
CINDEX
DIV
PUSHB_1
 3
CINDEX
PUSHB_1
 6
CINDEX
DIV
ROLL
SWAP
PUSHB_1
 5
CINDEX
PUSHB_1
 9
CINDEX
LT
IF
ADD
ROLL
ROLL
SUB
SWAP
PUSHB_1
 5
MINDEX
PUSHB_1
 5
MINDEX
PUSHB_1
 5
MINDEX
PUSHB_1
 7
MINDEX
ADD
ELSE
SUB
ROLL
ROLL
ADD
SWAP
PUSHB_1
 5
MINDEX
PUSHB_1
 5
MINDEX
PUSHB_1
 5
MINDEX
PUSHB_1
 7
MINDEX
SUB
EIF
PUSHW_1
 -85
JMPR
EIF
POP
POP
POP
PUSHW_1
 6745
DUP
ROLL
PUSHW_1
 4096
MUL
SWAP
DIV
ROLL
PUSHW_1
 4096
MUL
ROLL
DIV
ROLL
POP
EIF
EIF
ROLL
MUL
ROLL
ROLL
MUL
SWAP
ENDF

参考

*1:こんな風にMathJaxで数学記号が出せるのほんと楽しい。

2017-02-01

PPEM・ポイントサイズを表示するフォント

TrueType フォント

TrueType命令で遊ぶシリーズ。
前回までの記事はこちら:

何をするのか

ラスタライザのTrueType命令回りの挙動を見るのに便利かなあと思って、TrueType命令から取得できるPPEM(EMあたりのピクセル数)やポイント数を可視化できるようなフォントを作ってみる。

完成品

PPEM

f:id:nixeneko:20170129005803p:plain

Point Size

f:id:nixeneko:20170129005837p:plain

ダウンロード

PPEM表示: Appem.ttf (2.21 KB)
Point Size表示: Aps.ttf (2.20 KB)

尚、この記事の末尾にTrueType命令のソースコードをまとめて記載した。

追記(2017-02-01 4時ころ)

.@nixeneko こんなの見つけました。ご参考まで… ⁑ showcase · master · sev / f000 · GitLab https://t.co/BpKl9mmOvK
— mashabow (@mashabow) 2017年1月31日

gitlab.com
同様のものがすでにあったみたいですね。しかもこっちのが高機能だし……。

というか、PPEMは縦・横で異なる可能性があるのですね*1。長体・平体がかかった時は、確かに縦横でppemが異なりそう。

今回作成したものでは特にprojection vectorの指定をしてないので、MPPEMの前にSTVCA命令などでppemを計る軸を指定した方が良さそう。
(追記終)

方針

伝統ある7セグメント数字を使う。

一つの桁について、初めは8の字が表示されるように7つのセグメントを用意しておく。各セグメントには下図のように番号を割り振っておく。
f:id:nixeneko:20170129010346p:plain

このセグメントについて、その桁の数字が何であるかを見て、各セグメントを必要であれば適切に消去する。これによってその数字を構成するセグメントのみが残り、数字が表示できるという訳である。

	セグメントNo.	セグメントあり	セグメントなし
↑	0	0,2,3,5,6,7,8,9	1,4
↖	1	0,4,5,6,8,9	1,2,3,7
↗	2	0,1,2,3,4,7,8,9	5,6
－	3	2,3,4,5,6,8,9	0,1,7
↙	4	0,2,6,8	1,3,4,5,7,9
↘	5	0,1,3,4,5,6,7,8,9	2
↓	6	0,2,3,5,6,8,9	1,4,7

実装

次のようなグリフを用意した。
f:id:nixeneko:20170129011619p:plain
各セグメントは4つの制御点からなり、セグメントの並び順は上図の丸囲み数字の番号が若い順に並ぶようにした。
丸囲みの数字をセグメント番号sとすると、セグメントsは制御点4s～4s+3からなる。

また、四角で囲んだ数字(mとする)は、 $10^m$ の位の数字を表す。各桁に対応する数字位置におけるセグメントn ( $0 \le n \le 6$ )を考えると、
$s = 7m+n$
となるようになっている。

なお、セグメントの並べ替えは、.ttfに書き出し→ttxで.ttxに変換→テキストエディタで並べ替え→.ttfに変換という風にして行った。

関数0: 指定した制御点を原点に移動

次にTrueType命令を考えていく。
さて、まずは、以前作った、指定した番号の制御点を原点に移動する関数0をもってきて使うことにする。

PUSHB_1
0
FDEF
STVCA[1]
DUP
PUSHW_1
 0x0000
SCFS
STVCA[0]
PUSHW_1
 0x0000
SCFS
ENDF

関数1: 指定したセグメントを消去

次に、指定した番号のセグメントを消去する関数1を考える。
入力は消去したいセグメント番号sとする。
セグメント番号sは、右からm番目( $0 \le m \le 3$ )の数字のセグメントn ( $0 \le m \le 6$ )について $s = 7m+n$ で計算したものとする。
このとき、関数1は、制御点番号4s, 4s+1, 4s+2, 4s+3を原点に移動する。

/* func1: removes segment s */
/* initial stack ...|s|     */
/* final stack   ...|       */
PUSHB_1 1
FDEF        /* ...|s|                       */
PUSHW_1 256 /* ...|s|4.0|                   */
MUL         /* ...|4*s|                     */
DUP         /* ...|4*s|4*s|                 */
PUSHB_1 1   /* ...|4*s|4*s|1|               */
ADD         /* ...|4*s|4*s+1|               */
DUP         /* ...|4*s|4*s+1|4*s+1|         */
PUSHB_1 1   /* ...|4*s|4*s+1|4*s+1|1|       */
ADD         /* ...|4*s|4*s+1|4*s+2|         */
DUP         /* ...|4*s|4*s+1|4*s+2|4*s+2|   */
PUSHB_1 1   /* ...|4*s|4*s+1|4*s+2|4*s+2|1| */
ADD         /* ...|4*s|4*s+1|4*s+2|4*s+3|   */
PUSHB_1 0   /* ...|4*s|4*s+1|4*s+2|4*s+3|0| */
CALL        /* ...|4*s|4*s+1|4*s+2|         */ /*call func0 with 4*s+3*/
PUSHB_1 0   /* ...|4*s|4*s+1|4*s+2|0|       */
CALL        /* ...|4*s|4*s+1|               */ /*call func0 with 4*s+2*/
PUSHB_1 0   /* ...|4*s|4*s+1|0|             */
CALL        /* ...|4*s|                     */ /*call func0 with 4*s+1*/
PUSHB_1 0   /* ...|4*s|0|                   */
CALL        /* ...|                         */ /*call func0 with 4*s  */
ENDF

関数2: 各桁についての数字を表示

さて、次に、右からm番目( $0 \le m \le 3$ )の数字の値dについて適切にセグメントを消去する関数2を考える。これはまあ大体気合で。

/* func2: removes some segments of the m-th digit to show the number d */
/* initial stack ...|d|m| */
/* final stack   ...|     */
PUSHB_1 2
FDEF         /* ...|d|m|           */

PUSHW_1 448  /* ...|d|m|7.0|       */
MUL          /* ...|d|7*m|         */
SWAP         /* ...|7*m|d|         */

DUP          /* ...|7*m|d|d|       */
PUSHB_1 0    /* ...|7*m|d|d|0|     */
EQ           /* ...|7*m|d|d==0|    */
IF           /* ...|7*m|d|         */ /* if d==0 */ /* 消去: 3 */
  SWAP       /* ...|d|7*m|         */
  DUP        /* ...|d|7*m|7*m|     */
  PUSHB_1 3  /* ...|d|7*m|7*m|3|   */
  ADD        /* ...|d|7*m|7*m+3|   */
  PUSHB_1 1  /* ...|d|7*m|7*m+3|1| */
  CALL       /* ...|d|7*m|         */ /* call func1 with 7*m+3 */
  SWAP       /* ...|7*m|d|         */
EIF          /* ...|7*m|d|         */

DUP          /* ...|7*m|d|d|       */
PUSHB_1 1    /* ...|7*m|d|d|1|     */
EQ           /* ...|7*m|d|d==1|    */
IF           /* ...|7*m|d|         */ /* if d==1 */ /* 消去: 0,1,3,4,6 */
  SWAP       /* ...|d|7*m|         */
  DUP        /* ...|d|7*m|7*m|     */
  PUSHB_1 1  /* ...|d|7*m|7*m|1|   */
  CALL       /* ...|d|7*m|         */ /* call func1 with 7*m */
  DUP        /* ...|d|7*m|7*m|     */
  PUSHB_1 1  /* ...|d|7*m|7*m|1|   */
  ADD        /* ...|d|7*m|7*m+1|   */
  PUSHB_1 1  /* ...|d|7*m|7*m+1|1| */
  CALL       /* ...|d|7*m|         */ /* call func1 with 7*m+1 */
  DUP        /* ...|d|7*m|7*m|     */
  PUSHB_1 3  /* ...|d|7*m|7*m|3|   */
  ADD        /* ...|d|7*m|7*m+3|   */
  PUSHB_1 1  /* ...|d|7*m|7*m+3|1| */
  CALL       /* ...|d|7*m|         */ /* call func1 with 7*m+3 */
  DUP        /* ...|d|7*m|7*m|     */
  PUSHB_1 4  /* ...|d|7*m|7*m|4|   */
  ADD        /* ...|d|7*m|7*m+4|   */
  PUSHB_1 1  /* ...|d|7*m|7*m+4|1| */
  CALL       /* ...|d|7*m|         */ /* call func1 with 7*m+4 */
  DUP        /* ...|d|7*m|7*m|     */
  PUSHB_1 6  /* ...|d|7*m|7*m|6|   */
  ADD        /* ...|d|7*m|7*m+6|   */
  PUSHB_1 1  /* ...|d|7*m|7*m+6|1| */
  CALL       /* ...|d|7*m|         */ /* call func1 with 7*m+6 */
  SWAP       /* ...|7*m|d|         */
EIF          /* ...|7*m|d|         */

DUP          /* ...|7*m|d|d|       */
PUSHB_1 2    /* ...|7*m|d|d|2|     */
EQ           /* ...|7*m|d|d==2|    */
IF           /* ...|7*m|d|         */ /* if d==2 */ /* 消去: 1,5 */
  SWAP       /* ...|d|7*m|         */
  DUP        /* ...|d|7*m|7*m|     */
  PUSHB_1 1  /* ...|d|7*m|7*m|1|   */
  ADD        /* ...|d|7*m|7*m+1|   */
  PUSHB_1 1  /* ...|d|7*m|7*m+1|1| */
  CALL       /* ...|d|7*m|         */ /* call func1 with 7*m+1 */
  DUP        /* ...|d|7*m|7*m|     */
  PUSHB_1 5  /* ...|d|7*m|7*m|5|   */
  ADD        /* ...|d|7*m|7*m+5|   */
  PUSHB_1 1  /* ...|d|7*m|7*m+5|1| */
  CALL       /* ...|d|7*m|         */ /* call func1 with 7*m+5 */
  SWAP       /* ...|7*m|d|         */
EIF          /* ...|7*m|d|         */

DUP          /* ...|7*m|d|d|       */
PUSHB_1 3    /* ...|7*m|d|d|3|     */
EQ           /* ...|7*m|d|d==3|    */
IF           /* ...|7*m|d|         */ /* if d==3 */ /* 消去: 1,4 */
  SWAP       /* ...|d|7*m|         */
  DUP        /* ...|d|7*m|7*m|     */
  PUSHB_1 1  /* ...|d|7*m|7*m|1|   */
  ADD        /* ...|d|7*m|7*m+1|   */
  PUSHB_1 1  /* ...|d|7*m|7*m+1|1| */
  CALL       /* ...|d|7*m|         */ /* call func1 with 7*m+1 */
  DUP        /* ...|d|7*m|7*m|     */
  PUSHB_1 4  /* ...|d|7*m|7*m|4|   */
  ADD        /* ...|d|7*m|7*m+4|   */
  PUSHB_1 1  /* ...|d|7*m|7*m+4|1| */
  CALL       /* ...|d|7*m|         */ /* call func1 with 7*m+4 */
  SWAP       /* ...|7*m|d|         */
EIF          /* ...|7*m|d|         */

DUP          /* ...|7*m|d|d|       */
PUSHB_1 4    /* ...|7*m|d|d|4|     */
EQ           /* ...|7*m|d|d==4|    */
IF           /* ...|7*m|d|         */ /* if d==4 */ /* 消去: 0,4,6 */
  SWAP       /* ...|d|7*m|         */
  DUP        /* ...|d|7*m|7*m|     */
  PUSHB_1 1  /* ...|d|7*m|7*m|1|   */
  CALL       /* ...|d|7*m|         */ /* call func1 with 7*m */
  DUP        /* ...|d|7*m|7*m|     */
  PUSHB_1 4  /* ...|d|7*m|7*m|4|   */
  ADD        /* ...|d|7*m|7*m+4|   */
  PUSHB_1 1  /* ...|d|7*m|7*m+4|1| */
  CALL       /* ...|d|7*m|         */ /* call func1 with 7*m+4 */
  DUP        /* ...|d|7*m|7*m|     */
  PUSHB_1 6  /* ...|d|7*m|7*m|6|   */
  ADD        /* ...|d|7*m|7*m+6|   */
  PUSHB_1 1  /* ...|d|7*m|7*m+6|1| */
  CALL       /* ...|d|7*m|         */ /* call func1 with 7*m+6 */
  SWAP       /* ...|7*m|d|         */
EIF          /* ...|7*m|d|         */

DUP          /* ...|7*m|d|d|       */
PUSHB_1 5    /* ...|7*m|d|d|5|     */
EQ           /* ...|7*m|d|d==5|    */
IF           /* ...|7*m|d|         */ /* if d==5 */ /* 消去: 2,4 */
  SWAP       /* ...|d|7*m|         */
  DUP        /* ...|d|7*m|7*m|     */
  PUSHB_1 2  /* ...|d|7*m|7*m|2|   */
  ADD        /* ...|d|7*m|7*m+2|   */
  PUSHB_1 1  /* ...|d|7*m|7*m+2|1| */
  CALL       /* ...|d|7*m|         */ /* call func1 with 7*m+2 */
  DUP        /* ...|d|7*m|7*m|     */
  PUSHB_1 4  /* ...|d|7*m|7*m|4|   */
  ADD        /* ...|d|7*m|7*m+4|   */
  PUSHB_1 1  /* ...|d|7*m|7*m+4|1| */
  CALL       /* ...|d|7*m|         */ /* call func1 with 7*m+4 */
  SWAP       /* ...|7*m|d|         */
EIF          /* ...|7*m|d|         */

DUP          /* ...|7*m|d|d|       */
PUSHB_1 6    /* ...|7*m|d|d|6|     */
EQ           /* ...|7*m|d|d==6|    */
IF           /* ...|7*m|d|         */ /* if d==6 */ /* 消去: 2 */
  SWAP       /* ...|d|7*m|         */
  DUP        /* ...|d|7*m|7*m|     */
  PUSHB_1 2  /* ...|d|7*m|7*m|2|   */
  ADD        /* ...|d|7*m|7*m+2|   */
  PUSHB_1 1  /* ...|d|7*m|7*m+2|1| */
  CALL       /* ...|d|7*m|         */ /* call func1 with 7*m+2 */
  SWAP       /* ...|7*m|d|         */
EIF          /* ...|7*m|d|         */

DUP          /* ...|7*m|d|d|       */
PUSHB_1 7    /* ...|7*m|d|d|7|     */
EQ           /* ...|7*m|d|d==7|    */
IF           /* ...|7*m|d|         */ /* if d==7 */ /*消去: 1,3,4,6 */
  SWAP       /* ...|d|7*m|         */
  DUP        /* ...|d|7*m|7*m|     */
  PUSHB_1 1  /* ...|d|7*m|7*m|1|   */
  ADD        /* ...|d|7*m|7*m+1|   */
  PUSHB_1 1  /* ...|d|7*m|7*m+1|1| */
  CALL       /* ...|d|7*m|         */ /* call func1 with 7*m+1 */
  DUP        /* ...|d|7*m|7*m|     */
  PUSHB_1 3  /* ...|d|7*m|7*m|3|   */
  ADD        /* ...|d|7*m|7*m+3|   */
  PUSHB_1 1  /* ...|d|7*m|7*m+3|1| */
  CALL       /* ...|d|7*m|         */ /* call func1 with 7*m+3 */
  DUP        /* ...|d|7*m|7*m|     */
  PUSHB_1 4  /* ...|d|7*m|7*m|4|   */
  ADD        /* ...|d|7*m|7*m+4|   */
  PUSHB_1 1  /* ...|d|7*m|7*m+4|1| */
  CALL       /* ...|d|7*m|         */ /* call func1 with 7*m+4 */
  DUP        /* ...|d|7*m|7*m|     */
  PUSHB_1 6  /* ...|d|7*m|7*m|6|   */
  ADD        /* ...|d|7*m|7*m+6|   */
  PUSHB_1 1  /* ...|d|7*m|7*m+6|1| */
  CALL       /* ...|d|7*m|         */ /* call func1 with 7*m+6 */
  SWAP       /* ...|7*m|d|         */
EIF          /* ...|7*m|d|         */

                                      /*(if d==8)*/ /* 消去:なし */

DUP          /* ...|7*m|d|d|       */
PUSHB_1 9    /* ...|7*m|d|d|9|     */
EQ           /* ...|7*m|d|d==9|    */
IF           /* ...|7*m|d|         */ /* if d==9 */ /* 消去: 4 */
  SWAP       /* ...|d|7*m|         */
  DUP        /* ...|d|7*m|7*m|     */
  PUSHB_1 4  /* ...|d|7*m|7*m|4|   */
  ADD        /* ...|d|7*m|7*m+4|   */
  PUSHB_1 1  /* ...|d|7*m|7*m+4|1| */
  CALL       /* ...|d|7*m|         */ /* call func1 with 7*m+4 */
  SWAP       /* ...|7*m|d|         */
EIF          /* ...|7*m|d|         */

POP          /* ...|7*m|           */
POP          /* ...|               */
ENDF

数字で場合分けして、セグメントを消去する関数を呼び出してるというだけだが、全部スタックをつかって値を扱ってるので妙に長くなる。うーん、気合感。

関数3: 剰余の計算

次に、各桁の数値を計算して関数2を呼び出すような関数を作りたいところだが、先に剰余を計算する関数3を考える。

剰余の計算は、
$a \div b = c \ \mbox{余り} \ d$
のとき、
$a = bc + d$
が成り立つから、
$d = a -bc$
を計算すればいいことがわかる。cは結果が整数になる様な割り算 $c = \mathrm{int}(a/b)$ で求められるので、実際は
$d = a -b \cdot \mathrm{int}(a/b)$
といった感じの計算になる。

さて、関数を実装するが、ここで、MULやDIVは整数ではなくF26Dot6に対して定義されている命令であり、整数a, bに対して

MUL: a * b / 64
DIV: a * 64 / b

という風な計算になることに注意する。

/* func3: calculates remainder a % b */
/* initial stack: ...|dividend a(int)|divisor b(int)|          */
/*   final stack: ...|remainder(int) = dividend a % divisor b| */
PUSHB_1
 3
FDEF     /* ...|a|b|                 */
PUSHB_1  /* ...|a|b|2|               */
 2
CINDEX   /* ...|a|b|a|               */
PUSHB_1  /* ...|a|b|2|               */
 2
CINDEX   /* ...|a|b|a|b|             */
PUSHW_1  /* ...|a|b|a|b|64.0|        */
 4096
MUL      /* ...|a|b|a|b*64|          */
DIV      /* ...|a|b|int(a/b)|        */ /* DIV: (a)*64 / (b*64) */
PUSHB_1  /* ...|a|b|int(a/b)|1.0/64| */
 1
DIV      /* ...|a|b|int(a/b)*64|     */
MUL      /* ...|a|b*int(a/b)|        */ /* MUL: (b) * (int(a/b)*64) / 64 */
SUB      /* ...|a - b*int(a/b)|      */
ENDF

関数4: 数値を表示する

さて、ここで、各桁の数値を計算して関数2を呼び出し、数値を表示する関数4を作る。

要するに、数値xについて、
x%10, x/10 % 10, x/100 % 10, x/1000 % 10
を計算して、それらの数字が各桁に表示されるように関数2を適用する。 / は整数の除算、 % は剰余を表す。

/* func4: shows the given number x */
/* initial stack: ...|x|           */
/*   final stack: ...|             */
PUSHB_1 4
FDEF          /* ...|x|                  */
DUP           /* ...|x|x|                */
PUSHB_1 10 3  /* ...|x|x|10|3|           */
CALL          /* ...|x|x%10|             */ /*call func3 with x, 10 */
PUSHB_2 0 2   /* ...|x|x%10|0|2|         */
CALL          /* ...|x|                  */ /*call func2 with x%10, 0 */
PUSHW_1 640   /* ...|x|10.0|             */
DIV           /* ...|x/10|               */
DUP           /* ...|x/10|x/10|          */
PUSHB_2 10 3  /* ...|x/10|x/10|10|3|     */
CALL          /* ...|x/10|(x/10)%10|     */ /*call func3 with x/10, 10 */
PUSHB_2 1 2   /* ...|x/10|(x/10)%10|1|2| */
CALL          /* ...|x/10|               */ /*call func2 with (x/10)%10, 1 */
PUSHW_1 640   /* ...|x/10|10.0|          */
DIV           /* ...|x/100|              */
DUP           /* ...|x/100|x/100|        */
PUSHB_2 10 3  /* ...|x/100|x/100|10|3|   */
CALL          /* ...|x/100|(x/100)%10|   */ /*call func3 with x/100, 10 */
PUSHB_2 2 2   /* ...|x/100|(x/100)%10|2|2|   */
CALL          /* ...|x/100|              */ /*call func2 with (x/100)%10, 2 */
PUSHW_1 640   /* ...|x/100|10.0|         */
DIV           /* ...|x/1000|             */
DUP           /* ...|x/1000|x/1000|      */
PUSHB_2 10 3  /* ...|x/1000|x/1000|10|3| */
CALL          /* ...|x/1000|(x/1000)%10| */ /*call func3 with x/1000, 10 */
PUSHB_2 3 2   /* ...|x/1000|(x/1000)%10|3|2| */
CALL          /* ...|x/1000|             */ /*call func2 with (x/1000)%10, 3*/
POP           /* ...|                    */
ENDF

グリフのプログラム

さて、この関数4をグリフから呼び出す。
引数の数値としては、PPEMやポイントサイズを与えてみようと思う。

PPEM

PPEMとは、Pixels/EMのことで、EMのサイズが何ピクセルで描画されるかということを示した値である。

TrueType fundamentals - Typography | Microsoft Docsによると、ppemは、
ppem = pointSize * dpi / 72
によって計算される。

PPEMを測定するのはMPPEM命令を使う。PPEMを表示するようなプログラムは次のようになる。

MPPEM     /* |PPEM|   */
PUSHB_1 4 /* |PPEM|4| */
CALL      /* |        */ /* call func4 with PPEM */

ポイントサイズ

ポイントサイズを取得するのはMPS命令を使う。

MPS       /* |PS|   */ /* Point Size */
PUSHB_1 4 /* |PS|4| */
CALL      /* |      */ /* call func4 with PS */

いろんなソフトの挙動をみる

以下で挙げた他にも、Windows 10上のFirefox, Google Chromeでも動作するのを確認した。

Windows 10 フォントビューア

PPEM:
f:id:nixeneko:20170129005803p:plain

Point Size:
f:id:nixeneko:20170129005837p:plain
冒頭でも上げたが、PPEMとPoint Sizeが別の値を指している。PPEMの計算式から、DPIが96であることがわかる(要するに、72ptの時のPPEMがDPIである)。
なお、PPEMの値はディスプレイのDPI設定を変えると変わる。
まともな実装だと思う。

Ubuntu フォントビューア

gnome-tweak-toolでヒンティングを有効にしてある。

PPEM:
f:id:nixeneko:20170129164627p:plain

Point Size:
f:id:nixeneko:20170129164707p:plain

PPEMとポイントサイズが全く同じ値を示している。dpi=72固定ということだろうか。
システム設定→ディスプレイ→「メニューとタイトルバーの拡大縮小」をいじってみたけど変化なし。

Adobe ソフト

なんとAdobe IllustratorでもTrueType命令は動く。Photoshopでも動く。以下のスクリーンショットはWindows版のCS6のバージョンのものである。

Photoshop

PPEM:
f:id:nixeneko:20170129020643p:plain
謎の挙動を示す。上に挙げたppemの計算式に対し4掛けしたものが400以下かどうかで場合分けされるらしい。

if (4 * pointSize * dpi / 72 <= 400)
     ppem = 4 * pointSize * dpi / 72;
else
     ppem =     pointSize * dpi / 72;

みたいな感じか。

Point Size:
f:id:nixeneko:20170129020925p:plain
72固定っぽい。

Illustrator

Adobe Illustrator CS6 (Windows版)のPPEMの扱ひがキモい。一方Point sizeは72固定。 pic.twitter.com/EbB8NBPOwf
— にせねこ (@nixeneko) 2017年1月29日

Photoshopと似たような挙動を示す。

基本的に最終的に画面に表示されるサイズによってppemは計算される。ズームイン・ズームアウトでも値が変わる。
ドラッグで拡縮してるときはppemは(pointSize * dpi / 72)になり、マウスボタン離すと上のPhotoshopと同様の場合分けされた挙動をする。
ポイントサイズは、Shift+ドラッグによる拡縮時(つまり、長体あるいは平体がかかってない状態)では、72未満は反映されるが、マウスボタンを離すと72固定になる。
アウトライン化するときは、ppemは、100%表示にしたときのppemあるいは1024のどちらか大きい方になるっぽい。ポイントサイズは72固定。

InDesign

f:id:nixeneko:20170129163439p:plain
InDesignも、Illustratorと似た挙動をするっぽい。

基本的に最終的に画面に表示されるサイズによってppemは計算される。ズームイン・ズームアウトでも値が変わる。
ppemはPhotoshop同様に場合分けになるっぽい。
point sizeは72固定

After Effects

ppemは1024固定っぽい。
f:id:nixeneko:20170128105149p:plain
同様にPoint Sizeも72固定。
f:id:nixeneko:20170128112211p:plain

*1:MPPEMはprojection vectorを利用しているので。

2017-01-26

CygwinからNotepad++でファイルを開く: Unixパスの扱い

Cygwin

Cygwinでテキストファイルを編集したいとき、普段Windowsで使っているNotepad++を使ってコマンド一発で開ければ便利だなあと思った。
丁度Ubuntuでgeditを使うようなイメージで。

他のWindowsプログラムについても、同様に対応可能であると思う。

Notepad++の実行ファイルは次にある。

C:\Program Files (x86)\Notepad++\notepad++.exe

これはCygwinのUnixパスにすると

/cygdrive/c/Program Files (x86)/Notepad++/notepad++.exe

である。

案1

notepad++に実行ファイルのUnixフルパスをaliasしてみる。

alias notepad++='"/cygdrive/c/Program Files (x86)/Notepad++/notepad++.exe"'

内側をダブルクォートで囲んでいるのは、パスの中にスペースが含まれているため、そこで区切られて、ファイルが見つかりませんということになるのを避けるためである。

これだと、しかし、Unixパスで指定されたもの(“~/hoge”, “/usr/local/hoge”など)が開けない。これはNotepad++の実行ファイルにパスを通した場合でも同様だと思う。

案2

なので、引数が与えられた場合、cygpathを使ってWindowsパスに変換してから実行するような関数を作ってみた。

notepad++ () {
  if [ $# -eq 0 ]; then
    '/cygdrive/c/Program Files (x86)/Notepad++/notepad++.exe' &
  else
    for x in "$@"; do
      '/cygdrive/c/Program Files (x86)/Notepad++/notepad++.exe' "`cygpath -wa \"$x\"`" &
    done
  fi
}

引数の個数が0ならそのまま実行し、そうでなければすべての引数についてcygpathでWindowsフルパスに変換したものを引数として与えて実行している。
Notepad++のプログラムは & をつけてバックグラウンドで実行されるようにした。これをしないと複数ファイルを開けないからである。

~/.bashrc に書いておいた。

さて、とりあえず動いているのだが、これでいいのかどうか。

参考

2017-01-21

Undertaleをやろうとしたらゲームパッドの上が効かない

ゲーム Windows

環境

OS: Windows 10
ゲームパッド: Buffalo Classic USB Gamepad BSGP801

症状

ゲームパッドを接続してUndertaleを起動したところ、ゲームパッド十字キーの上が押しても反応せず、右左下には動けるのに上には動けない、あるいは上がずっと押しっぱなし状態になるかのどちらかで困っていた。
なお、別のスーファミ風ゲームパッド(Elecom 8 Button Gamepad JC-FR08T)でも同様の状態になった。

解決策

UndertaleのJoystick Configを開き、DIR CHOICEをANALOG ONLYに変更。
f:id:nixeneko:20170121111745p:plain

POVによる入力はうまく動かないようで、Analog入力を使うように設定しないといけないっぽい。

ゲームパッドの十字キー上方向の入力が効く、この当たり前のことが、あなたを決意でいっぱいにした。